Lösung von Aufgabe 7.1 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
Lösungsvorschlag:
 
Lösungsvorschlag:
  
−
a) AB+ n BA+ = Die Strecke AB
+
a) AB<sup>+</sup> <math>\cap</math> BA<sup>+</sup> = <math>\overline {AB}</math><br />
−
b) AB- n BA- = {}
+
b) AB<sup>-</sup> <math>\cap</math> BA<sup>-</sup> = {}<br />
−
c) AB geschnitten mit dem Kreis um A durch B = B,X und |AX| = |AB| (man sollte noch ergänzen, dass X auf AB liegt und X <math>X \neq B</math> gilt.--[[Benutzer:Andreas|Tutor Andreas]] 12:36, 19. Jun. 2012 (CEST)
+
c) AB geschnitten mit dem Kreis um A durch B = B,X und |AX| = |AB| (man sollte noch ergänzen, dass X auf AB liegt und <math>X \neq B</math> gilt.--[[Benutzer:Andreas|Tutor Andreas]] 12:36, 19. Jun. 2012 (CEST)<br />
−
d) AB n BA = AB (AB und BA sind identisch)
+
d) AB <math>\cap</math> BA = AB (AB und BA sind identisch)<br />
  
−
(n bedeutet "geschnitten")
 
  
 
--[[Benutzer:RitterSport|RitterSport]] 19:07, 9. Jun. 2012 (CEST)
 
--[[Benutzer:RitterSport|RitterSport]] 19:07, 9. Jun. 2012 (CEST)
  
−
a) = Strecke AB
+
a) = <math>\overline {AB}</math><br />
−
b) Alle Punkte außer die Strecke, also die leere Menge. ={ }
+
b) Alle Punkte außer die Strecke, also die leere Menge. ={ }<br />
 +
*Also das finde ich jetzt etwas verwirrend, denn alle Punkte außer einer STrecke sind ganz viele Punkte und nicht die leere Menge. Man muss sich genau ausdrücken, denn sonst passiert so etwas :)--[[Benutzer:Andreas|Tutor Andreas]] 12:45, 19. Jun. 2012 (CEST)<br />
 
c) Da Punkt A nicht Element seines eigenen Kreises ist, ist die Menge leer. = { }
 
c) Da Punkt A nicht Element seines eigenen Kreises ist, ist die Menge leer. = { }
 +
*Das stimmt so nicht. Hier die Skizze dazu.<br />
 +
<ggb_applet width="537" height="321"  version="4.0" ggbBase64="UEsDBBQACAgIAKhl00AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAKhl00AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVhtb9s2EP7c/oqDPte2KEqyXNgt3BTFCqTtgHTDsG+URNusJVET6begP35HUrLlJE2zJCgWxOHLHe94z73Rmb7dlwVseaOErGYeGfoe8CqTuaiWM2+jF4PEe/vm5XTJ5ZKnDYOFbEqmZ15oOEU+8yZksQjSSTSIQxoPwthPBmkY8IHvL2iQBTTKwtAD2CvxupKfWclVzTJ+la14yS5lxrRVvNK6fj0a7Xa7YadqKJvlaLlMh3uVe4DXrNTMayevUdzZoR217IHvk9Ffny6d+IGolGZVxj0wJmzEm5cvpjtR5XIHO5Hr1cyLIurBiovlytgUJR6MDFONgNQ802LLFR7tLa3Nuqw9y8YqQ3/hZlAczfEgF1uR82bm+UMakzimcRQkfpBMKCqUjeCVbnlJq3PUSZtuBd85sWZmNSKEWsoiZUYifP8OgR/48MoMxA0BDnHsSL7b86kbAjeEbogcT+iOh441dDyh4wnxjluhRFrwmbdghUIERbVo0HvHtdKHgtv7tBsn68krtEmJa2SmPoaJgxz3ff+V+cT4CQ1hdG4k6WnVzeY/Ku1URnT8cJXBkwylnc7gLjOD6AdmxvcodXY/xE4S9XSiKvtrP7c00vvMvKnRrZ+mMA5/iYnTUZcq0zY7QK0Mbxs9mpfK5AudQDQxYU8gwtyIxxjlEZAJDuMAMBuARBBGuCQJxGYcAx0jIQQKCRg+QsEmR5Tgn3BshcUQoTCzO8acBIKKQogoEJtTIWAmgc1LzNGAIkcUQYSHjHoSGBE0hjDGFU0gxDualBwTZKR4ENeoPgBKgJrDZAxBDLGRR0KT6nFiro4iA4h9iIkRiFmNGe2yGfkToMaauIVLVPVGn0GUlXk31bI++gK5sR6dqp6rT2dF8cW0YCkvsE9cGU8CbFlhMsIqWshKQ+fEwO0tG1avRKauuNZ4SsE3tmWXTPP9B+RWnW7Lm8lK/d5IfSGLTVkpgEwW/vHOsiC9eXC8NS5ojxD2CVGPEPfm4zv1SqTARnHULxvVsbM8/2g4TqUBkfxSFYd3DWfrWopzM6Yj23KmfJMVIhes+hOD1WgxuMCxA5ly1XWgYEK7i8gmvzoojGDY/80baWjYc/s/6NWDI9GADCf9H0w/lTGTfJF/fggrwaElhZPzQ4lTzbdHD7E9Pxm7bExm9xYf1TtZnLas/Res1pvGPh6wODbGqnm1LLiNEVtusTNn61Tur1xwUCfr66HGle9ukC4t7oC1IYgiZGjH1I2Wx1ztyOVbHt9y+F20ifxIJ5PActgxdaPlwvB1V2tNJZ2ZxO/UCGUrmu+1edNVKxP8ptFvKqEvu4UW2bo1lbgDnzdlyo8hdC6TPJfM6ehGjE3XvKl40YY0OnMjN8plaC/ac56JEpeO0ELCjLv+wAu43ZwvG95dvLAPMweYpfr9aL21bUV9aGT5sdp+xVi4cYHpqLvlVGWNqE3MQYptYM1PUZULxbCL5P1zJgfR9Mx0C4RHG2gwOzd6JRv79sKigqNJvYKX+NICbcPLRugR5rl9whk8QabfsK4dW5+jnxyG5DtDzQYlK+oVM8+81uiCHXhzBoOV90nmN8FB7K0FmOS1EWC8W3PuAsPdGCc1CrT5dFamEG8F+5k3CIbEpDReZjjx4No94d0b1lhrsuysMrvdG67C+HFA/QSyd/8vyB4FmMXZ4jV+FrwyWZasyqGyb5tLLCjeqdUy38QZMGKwc8BsdEdgTlQr4Bb0pjYdkWU/Qb5n64+g9x8P/Ak+RO+sZ0zGtEXTdBaEcxANQxr2Gg65WWk1PgLW+E1H2Xag28JvJ7+JPOf2Aeg60T+VO6Jc+RNlXYhM6PtdcCGarHiwE9b3OwFLjciOKK+fHP8Pd8KXxUJx7XI8sRgPupfU3U56FMJiyastGoKvHPyO7rf/ATj47n5w3e3siU0dQyPt1jXpJQ/mZSP2MO/45x3XHJ9nyXCc4ItkTlup89AEjKlb88iWsMnd/javTbFA/O/198dKYzNEG264fO1czm65/MIR3t/v+fPKd/Eoz5uvQUs3pG54egY+ewG7z+z3v9bsfsy3XY0+EJVwSPpVx3cYUYPVM2A06j857Mu+/SfVm38BUEsHCJ/wnUsnBgAAQRMAAFBLAQIUABQACAgIAKhl00DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAqGXTQJ/wnUsnBgAAQRMAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAC+BgAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br />--[[Benutzer:Andreas|Tutor Andreas]] 12:45, 19. Jun. 2012 (CEST)<br />
 +
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 15:59, 12. Jun. 2012 (CEST)<br />
 
d) = {A,B}
 
d) = {A,B}
−
--[[Benutzer:Luca123|Luca123]] 20:00, 10.Jun. 2012 (CEST)
+
--[[Benutzer:Luca123|Luca123]] 20:00, 10.Jun. 2012 (CEST)<br />
  
  
−
Dito
+
Dito,außer bei c) {B}
−
Außer bei  
+
Strecke <math>\overline {AB}</math> ist der Kreisradius und somit ist B in beiden Punktmengen enthalten. <br />
−
 
+
−
c) {B}
+
−
Strecke AB ist der kreisradius somit ist B in beiden enthalten
+
−
<br />
+
  
 
'''Gedanke Nummero6/Tchu Tcha Tcha:'''<br />
 
'''Gedanke Nummero6/Tchu Tcha Tcha:'''<br />
 
Ich gebe RitterSport meine Stimme ;-)<br />
 
Ich gebe RitterSport meine Stimme ;-)<br />
−
Bsp. für c):<br />
 
−
<ggb_applet width="784" height="463"  version="4.0" ggbBase64="UEsDBBQACAAIAI9+zEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAI9+zEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vjrj9M4EP8Mf8Uon7dpHDsv1IIWJHRIC5y03Ol039zEbc0mcS5xXyv++BvbSZuWZeEA3ekkFsee8Tx+8/Dszl7sqxK2ou2kquce8QMPRJ2rQtarubfRy0nqvXj+dLYSaiUWLYelaiuu5x4znLKYe0maFQnj+SSOaTFhAUsmaZHHE0ZETPOck2gpPIB9J5/V6h2vRNfwXNzma1HxG5VzbRWvtW6eTae73c4fVPmqXU1Xq4W/7woP0My6m3v9xzMUd3ZpRy17GARk+sfbGyd+IutO8zpH/caFjXz+9MlsJ+tC7WAnC72ee2mAbqyFXK3Rp9hspoapQUAakWu5FR1eHW2tz7pqPMvGa0N/4r6gPLrjQSG3shDt3Av8MPJAtVLUuqeSXst0uD/bSrFzgsyX1cE80EqVC25kwKdPEAZhAFdmIW4JcYljRwrcWUDdErqFuSVyPMxdZ46VOR7meBj1YCs7uSjF3FvyskPMZL1sMV7HfacPpbD29Acnf8kV+tTJe2SmBkQHMp4HwZX5QWSv2IDuyEky0qrbzT9UOqhMUvbtKsMfcpQOOsOH3AyjL7gZP6LU+f0tfpJopBNV2X/25zON9DE3LzW6/Y8pjNm/4uJsOpTKrK8O6NaGt88eLarO1AvNIMpM2hOIsDbiBLM8ApLhkoSA1QAkAhbhlqQQmzUBmiCBAYUUDB+hYIsjSvE/llhhMUQozJwmWJNAUBGDiAKxNcUAKwlsXWKNhhQ5oggivGTUk9CIoDGwGHc0BYY2mpJMCDJSvIh7VB8CJUDNZZJAGENs5BFmSj1OjekoMoQ4gJgYgVjVWNGumpE/BWq8iXu4ZN1s9BlEeVUMn1o1x1ggN/ajU59z/emsDT6ZlXwhSnwZbk0kAba8NBVhFS1VrWEIYujOVi1v1jLvboXWeKuDj3zLb7gW+9fI3Q26LW+u6u7XVulXqtxUdQeQqzI42qxKMvoOj1bjho4IbEyIRoR49J08qFchBTadQP2q7QZ2XhRvDMepNSCS7+vy8LIV/K5R8tyN2dQ+MjOxyUtZSF7/jslqtBhcYHhzbLsa3hxGo8EQ1Ra3hw4zGPZ/ilYhtCTx0zQjURxnYRLSBKN6cKSQxX7GWEwTmtGE0ChF23Juii9M/QjPMhrTLEzDBFvW4Qsk0usW22OI+F6cvF21prRHmzfdS1WejiwAr3ijN62dF1BVa9y6rlelsEli+y0+xvndQu1vXXZQJ+vDocFd4CxYrCzwgM0hjPC9XPXrwq2Wx5h25AosT2A5giHdZHGkkyy0HHZduNVyYf4603pXyeAmCQY1srMtLfD6whnalcl+87Zvaqlvho2W+V3vKnEX3m2qhTjm0LlM8rNkzqYXSTa7E20tyj6nMZgbtelciY7SvRC5rHDrCD0k3ITrNzTAnRZi1YrB8NLOYg4wSw3G6frZsRX1ulXVm3r7AXPhwoDZdLBy1uWtbEzOwQLfgTtxyqpCdhyfkWJ8zxQhup6b5wLh0QYaLM+NXqvWjlvYVXA1tVeKCkct0Da9bIYeYb62U5vBE9TiIza249vn6KeAIfnBVLNJyctmzc1k1ztd8oNoz2Cw8t6q4hIcxN56gFXeuNg2Qri0cPbiR4PibDWddSlEu4P93JsQP8KMPqApPsGiv3dDu5tajbOmyM46szu9iBSmj8PpK4i9/P8jxnzGIpplSZQwHJqDzKJHfZrhRJxiA00JDbOM/hQsc1VVvC6gtnPPDfYa7/QM88CkIHBicHWgbfRA4E5UL+CzsJi2dUSdfyUqIxy+FJbg+4NylowhOUORWHAjP4vHkLs8nRDmp4zh00MQbkoDSi5bssZx4Q5/J+rsu6H7F8J+/CKLQthR0T1Zf9XuSuf6pKyaUuZSPx6QV7LNy28OSf54SLAnyfyIef6fxuS7IJQrUW/RUhx48Bf0oP/1/xA4/XA/nOwRnYk9OpD+6J6MagVLtJV7uB74rweua5zUJmHmZ2mK40acJQEhcZIggfY6rplhNR3tOjK8pqc9GF8zh8qlzC/jOx2/DHYC6/988PxvUEsHCHPaLmP6BQAA2xAAAFBLAQIUABQACAAIAI9+zEDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAj37MQHPaLmP6BQAA2xAAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACRBgAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br />
 
−
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 15:59, 12. Jun. 2012 (CEST)
 
  
  
−
__________________________________________________________________________________________________
 
−
_____________________________________
 
 
Was soll man da noch sagen. Wieder was gelernt!  
 
Was soll man da noch sagen. Wieder was gelernt!  
 
--[[Benutzer:Luca123|Luca123]]23:31, 14.Jun. 2012 (CEST)
 
--[[Benutzer:Luca123|Luca123]]23:31, 14.Jun. 2012 (CEST)
 +
 +
*Als Übung könnte jemand oder der Autor selbst, den Beitrag von Luca123 verbessern. --[[Benutzer:Andreas|Tutor Andreas]] 12:51, 19. Jun. 2012 (CEST)

Aktuelle Version vom 1. Juli 2012, 16:02 Uhr

Lösungsvorschlag:

a) AB+ 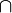\cap BA+ = \overline {AB}
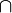b) AB- \cap BA- = {}
c) AB geschnitten mit dem Kreis um A durch B = B,X und |AX| = |AB| (man sollte noch ergänzen, dass X auf AB liegt und 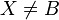X \neq B gilt.--Tutor Andreas 12:36, 19. Jun. 2012 (CEST)
d) AB 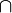\cap BA = AB (AB und BA sind identisch)


--RitterSport 19:07, 9. Jun. 2012 (CEST)

a) = \overline {AB}
b) Alle Punkte außer die Strecke, also die leere Menge. ={ }

  • Also das finde ich jetzt etwas verwirrend, denn alle Punkte außer einer STrecke sind ganz viele Punkte und nicht die leere Menge. Man muss sich genau ausdrücken, denn sonst passiert so etwas :)--Tutor Andreas 12:45, 19. Jun. 2012 (CEST)

c) Da Punkt A nicht Element seines eigenen Kreises ist, ist die Menge leer. = { }

  • Das stimmt so nicht. Hier die Skizze dazu.


--Tutor Andreas 12:45, 19. Jun. 2012 (CEST)

--Tchu Tcha Tcha 15:59, 12. Jun. 2012 (CEST)
d) = {A,B} --Luca123 20:00, 10.Jun. 2012 (CEST)


Dito,außer bei c) {B} Strecke \overline {AB} ist der Kreisradius und somit ist B in beiden Punktmengen enthalten.

Gedanke Nummero6/Tchu Tcha Tcha:
Ich gebe RitterSport meine Stimme ;-)


Was soll man da noch sagen. Wieder was gelernt! --Luca12323:31, 14.Jun. 2012 (CEST)

  • Als Übung könnte jemand oder der Autor selbst, den Beitrag von Luca123 verbessern. --Tutor Andreas 12:51, 19. Jun. 2012 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_7.1_S_(SoSe_12)&oldid=15766“