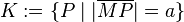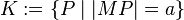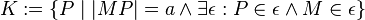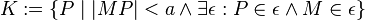Übung vom 13.05.11: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 01) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 01) |
||
| Zeile 6: | Zeile 6: | ||
# <math>K:= \lbrace P \mid | \overline{MP} | = a \rbrace</math> | # <math>K:= \lbrace P \mid | \overline{MP} | = a \rbrace</math> | ||
# <math>K:= \lbrace P \mid | MP | = a \rbrace</math> | # <math>K:= \lbrace P \mid | MP | = a \rbrace</math> | ||
| − | # <math>K:= \lbrace P \mid | MP | = a \wedge \exist \epsilon: P\in \epsilon \ | + | # <math>K:= \lbrace P \mid | MP | = a \wedge \exist \epsilon: P\in \epsilon \wedge M \in \epsilon \rbrace</math> |
| − | # <math>K:= \lbrace P \mid | MP | < a \ | + | # <math>K:= \lbrace P \mid | MP | < a \wedge \exist \epsilon: P\in \epsilon \wedge M \in \epsilon \rbrace</math> |
Korrekte Lösung aus der Übung:<br /> | Korrekte Lösung aus der Übung:<br /> | ||
<iframe src="http://www.ph-heidelberg.de/wp/gieding/Uebungen/Uebung_01/Neuer%20Ordner/Student%20Submissions_001.png" width="720" height="540" frameborder="2"></iframe><br /> | <iframe src="http://www.ph-heidelberg.de/wp/gieding/Uebungen/Uebung_01/Neuer%20Ordner/Student%20Submissions_001.png" width="720" height="540" frameborder="2"></iframe><br /> | ||
Version vom 8. Juli 2012, 23:24 Uhr
Inhaltsverzeichnis |
Übung vom 13.05.2011
Aufgabe 01
Ein Kreis ist die Menge aller Punkte einer Ebene 
, die zu einem gegebenen Punkt dieser Ebene ein und denselben Abstand haben.
Es seien 
ein beliebiger Punkt des Raumes und 
eine positive reelle Zahl. Im Folgenden wird jeweils eine Menge von Punkten definiert, die sich auf und beziehen. Welche der Mengen ist ein Kreis?
Korrekte Lösung aus der Übung:
[ www.ph-heidelberg.de is not an authorized iframe site ]
Aufgabe 02
Wir setzen ebene Geometrie voraus.
Es seien 
und 
zwei verschiedene Punkte der Ebene.
Was für ein geometrisches Objekt wird durch die folgende Menge definiert?
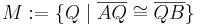
Nicht korrekte Lösung:
[ www.ph-heidelberg.de is not an authorized iframe site ]
Aufgabe: Formulieren Sie Aufgabe 02 derart, dass obige Antwort korrekt wäre.
korrekte Lösung:
[ www.ph-heidelberg.de is not an authorized iframe site ]
Aufgabe: Die Anwort ist richtig, die Skizze aus didaktischer Sicht suboptimal. Wie könnte man die Skizze optimaler gestalten.(s. Auftrag der Woche 8 (SoSe 11))
Aufgabe 03
Formulieren Sie eine Definition des Begriffs Mittelsenkrechte einer Strecke, die die Semantik der Begriffsbezeichnung verwendet.
Erklärung: Semantik meint hier, die Bedeutung der Begriffsbezeichnung wird in der Definition aufgegriffen.
- Warum sind die folgenden Antworten nicht korrekt bezüglich der Aufgabenstellung?
(A)
[ www.ph-heidelberg.de is not an authorized iframe site ]
(B)
[ www.ph-heidelberg.de is not an authorized iframe site ]
- Fast richtig, die Aufgabe wurde letztendlich jedoch nicht völlig korrekt gelöst. Warum?
- Diskutieren Sie den Gebrauch des unbestimmten Artikels.
[ www.ph-heidelberg.de is not an authorized iframe site ]
- korrekt:
[ www.ph-heidelberg.de is not an authorized iframe site ]
Aufgabe 04
Was stört Sie an der folgenden Definition?
- Definition: Wenn es eine Symmetrieachse gibt, so ist das Viereck ein gleichschenkliges Trapez.
- Korrekt! Diskutieren Sie warum!
- Die Frage wurde gleich zweimal korrekt beantwortet. Klar?
[ www.ph-heidelberg.de is not an authorized iframe site ]
- Hier wurde die Sache mit der Verwendung von Existenzaussagen in Definitionen nicht ganz verstanden. Warum?
[ www.ph-heidelberg.de is not an authorized iframe site ]
- Die Frage "welches?" hätte zur korrekten Antwort gereicht. Ist Ihnen klar warum?
[ www.ph-heidelberg.de is not an authorized iframe site ]
- Korrekt!
[ www.ph-heidelberg.de is not an authorized iframe site ]
