Lösung von Aufgabe 9.1 S: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Kommentar M.G.) |
*m.g.* (Diskussion | Beiträge) (→Die Augabe) |
||
| (9 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Die | + | ==Die Aufgabe== |
Definieren Sie den Begriff ''Inneres eines Dreiecks''.<br /> | Definieren Sie den Begriff ''Inneres eines Dreiecks''.<br /> | ||
<br /> | <br /> | ||
| + | |||
==Definitionsversuch Nummero6/Tchu Tcha Tcha:== | ==Definitionsversuch Nummero6/Tchu Tcha Tcha:== | ||
Es sei ein Dreieck ABC. Die Schnittmenge des Inneren der Winkel <math>\angle CAB , \angle ABC und \angle BCA</math> nennt man das "Innere eines Dreiecks".<br /> | Es sei ein Dreieck ABC. Die Schnittmenge des Inneren der Winkel <math>\angle CAB , \angle ABC und \angle BCA</math> nennt man das "Innere eines Dreiecks".<br /> | ||
| Zeile 10: | Zeile 11: | ||
* '''Es sei ein Dreieck <math>\overline{ABC}</math>.''' | * '''Es sei ein Dreieck <math>\overline{ABC}</math>.''' | ||
:::Hier kann man den unbestimmten Artikel "ein" wählen. Man muss es jedoch nicht. Es würde auch gehen: Gegeben sei das Dreieck <math>\overline{ABC}</math>. ''Das Dreieck'' steht für alle Dreiecke. ''Das Dreieck'' ist damit ein beliebiges Dreieck.<br /> | :::Hier kann man den unbestimmten Artikel "ein" wählen. Man muss es jedoch nicht. Es würde auch gehen: Gegeben sei das Dreieck <math>\overline{ABC}</math>. ''Das Dreieck'' steht für alle Dreiecke. ''Das Dreieck'' ist damit ein beliebiges Dreieck.<br /> | ||
| − | :::Was nicht so richtig zusammenpasst ist ihr Satzbau: Es sei ein Dreieck ... . Aus rein syntaktischer Sicht müsste das Wort ''Dreieck'' das Subjekt in ihrem Satz sein. (Satz im Sinne der deutschen Sprache und nicht als wahre Aussage der Mathematik.) Nach dem Subjekt ''Dreieck'' müsste ein Objekt kommen. Also etwas, was auf die Frage "Was sei ein Dreieck?" als Antwort dienen kann. Es folgt die Bezeichnung <math>\overline{ABC}</math>. Das passt so nicht ganz. Das wäre etwa dasselbe wie: Es sei ein Mensch Kevin. Das würde niemand sagen. Wir würden eher formulieren: Es sei ein Mensch namens Kevin. Hört sich auch blöd an. In dem Satz fehlt einfach was. Etwa sowas: Wir gehen davon aus, dass ein Mensch namens Kevin auch da ist. Mit unserem Dreieck wird es einfacher : Gegeben sei ein Dreieck <math>\overline{ABC}</math>. Wenn wir auf das ''gegeben'' verzichten wollen, müssen wir umstellen. Es sei <math>\overline{ABC}</math> ein Dreieck. Wer oder was sei ein Dreieck? <math>\overline{ABC}</math>. Was sei <math>\overline{ABC}</math>? ein Dreieck. Analog: Es sei Kevin ein Mensch. Das macht Sinn. Unser Hund heißt z.B. Fritz. Seit den 90ger Jahren und den Back Street Boys | + | :::Was nicht so richtig zusammenpasst ist ihr Satzbau: Es sei ein Dreieck ... . Aus rein syntaktischer Sicht müsste das Wort ''Dreieck'' das Subjekt in ihrem Satz sein. (Satz im Sinne der deutschen Sprache und nicht als wahre Aussage der Mathematik.) Nach dem Subjekt ''Dreieck'' müsste ein Objekt kommen. Also etwas, was auf die Frage "Was sei ein Dreieck?" als Antwort dienen kann. Es folgt die Bezeichnung <math>\overline{ABC}</math>. Das passt so nicht ganz. Das wäre etwa dasselbe wie: Es sei ein Mensch Kevin. Das würde niemand sagen. Wir würden eher formulieren: Es sei ein Mensch namens Kevin. Hört sich auch blöd an. In dem Satz fehlt einfach was. Etwa sowas: Wir gehen davon aus, dass ein Mensch namens Kevin auch da ist. Mit unserem Dreieck wird es einfacher : Gegeben sei ein Dreieck <math>\overline{ABC}</math>. Wenn wir auf das ''gegeben'' verzichten wollen, müssen wir umstellen. Es sei <math>\overline{ABC}</math> ein Dreieck. Wer oder was sei ein Dreieck? <math>\overline{ABC}</math>. Was sei <math>\overline{ABC}</math>? ein Dreieck. Analog: Es sei Kevin ein Mensch. Das macht Sinn. Unser Hund heißt z.B. Fritz. Seit den 90ger Jahren und den Back Street Boys muss man mit dem Namen Kevin vorsichtig sein. Manch einer behauptet, dass Kevin kein Name mehr ist, sondern eine Diagnose. |
:::Also korrekt wäre: Es sei <math>\overline{ABC}</math>ein Dreieck. | :::Also korrekt wäre: Es sei <math>\overline{ABC}</math>ein Dreieck. | ||
| Zeile 33: | Zeile 34: | ||
# Würde die Definition auch ohne die explizite Verwendung der Inneren der Winkel definieren können. | # Würde die Definition auch ohne die explizite Verwendung der Inneren der Winkel definieren können. | ||
--[[Benutzer:*m.g.*|*m.g.*]] 23:47, 20. Jun. 2012 (CEST) | --[[Benutzer:*m.g.*|*m.g.*]] 23:47, 20. Jun. 2012 (CEST) | ||
| + | <br /> | ||
| + | 1) Nein, stimmt. Anhand von 2 Innenwinkeln kann man das "Innere eines Dreiecks" definieren.<br /> | ||
| + | 2) Es sei <math>\overline{ABC}</math> ein Dreieck. Die Schnittmenge der drei Halbebenen <math>\ BC, A^{+}</math>, <math>\ AB, C^{+}</math> und <math>\ AC, B^{+}</math> nennt man das "Innere des Dreiecks <math>\overline{ABC}</math> ".<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 07:06, 21. Jun. 2012 (CEST) | ||
| + | perfekt--[[Benutzer:*m.g.*|*m.g.*]] 10:23, 21. Jun. 2012 (CEST) | ||
| + | [[Kategorie:Einführung_S]]<br /> | ||
| − | [[ | + | |
| + | |||
| + | == Just noch ein sailA == | ||
| + | <br /> | ||
| + | === '''Vorschlag 1''' === | ||
| + | <br /> | ||
| + | <math>\overline{ABC}</math> sei ein Dreieck.<br /> | ||
| + | Die Menge aller Punkte<math>\ I := \{P|P\in \ AB,C^{+}\cap\ BC,A^{+} \cap\ AC,B^{+} \}</math> <br /> | ||
| + | ist Inneres des Dreiecks.<br />--[[Benutzer:Just noch ein sailA|Just noch ein sailA]] 14:55, 25. Jun. 2012 (CEST)<br /> | ||
| + | |||
| + | == Kopernikus == | ||
| + | <br /> | ||
| + | === '''Vorschlag 1''' === | ||
| + | <br /> | ||
| + | Die Punkte der Schnittmenge zweier Innenwinkel eines Dreieckes nennt man Inneres des Dreiecks.<br /> | ||
| + | --[[Benutzer:Kopernikus|Kopernikus]] 14:53, 25. Jun. 2012 (CEST)<br /> | ||
| + | Das stimmt so nicht. Was sind denn Winkel? Ein Winkel besteht aus zwei Strahlen. Bilde ich nun den Schnitt von zwei Innenwinkeln eines Dreiecks, so erhält man eine Seite des Dreiecks und einen Eckpunkt, der nicht zu dieser Seite gehört. Nicht aber das Inneredes Dreiecks. Hier eine Skizze als Verdeutlichung...<br /> | ||
| + | <ggb_applet width="559" height="317" version="4.0" ggbBase64="UEsDBBQACAgIAKWN4UAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAKWN4UAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vlbb9s2FH5ufwWh51oWJVGyC7tFE6BYgN6wdMOwN0qiZTaSqIn0reiP3yEpybKdpk7bDUmDOhTFw3P9ziXu7OW2LNCaNZKLau5g13MQq1KR8SqfOyu1GE2cly+eznImcpY0FC1EU1I1d0JNybO5k2RBMl0EdBRP03QUhlE6on7ojQLqLWKSEJyFkYPQVvLnlXhHSyZrmrLrdMlK+kakVBnBS6Xq5+PxZrNxO1GuaPJxnifuVmYOAjUrOXfah+fA7uDSJjDkvufh8V9v31j2I15JRauUOUibsOIvnj6ZbXiViQ3a8Ewt5w6JiYOWjOdLbRMJHTTWRDU4pGap4msm4epga2xWZe0YMlrp8yf2CRW9OQ7K+JpnrJk7nhuE8cSPvEk0JRHxcRw4SDScVaolxq3QccdutuZsY/nqJyMSNFNCFAnVLNGXL8j3fA890wu2iw9LFNkjz77zArv4dgntQixNaK+HljS0NKGlCUHHNZc8KdjcWdBCggt5tWggfP1eql3BjD7ti735+BnYJPlnIA48wIn1Obz3vGf6E8En1AfjQyPxQKpqVvcU2okkZHq+SP+HDA06mf5tZvrkK2ZGdwi1dp9jJyYDmSDK/DOfE4nBXWYeS7T7HxMYhf+LibNxlyqzNjuQXGraFj2KlVLnSzBFZKphjxGB3IhiQDlBeApL7CPIBoQJCgls8QRFeo1REMNBiAI0QZoOB8gkB5nArzA2zCJEgJl+G0NOIgyCQkQChE1OhQgyCZm8hBz1A6AgBBG4pMVjX7MIIhRGsAsmKAQddUrGGAgDuAh7EO+jAKNAX8Yx8iMUaX441KkeTbTqwNJHkYcirBlCVkNG22wG+gkKtDVR6y5e1St14KK0zLpHJeo+FkAN9Whf9mx9OqiKT2YFTVgBjeJaRxKhNS10RhhBC1Ep1AXRt+/yhtZLnsprphTckugTXdM3VLHta6CWnWxDm4pKfmiEuhTFqqwkQqkovF5nUeDBs99rDZtgcBAOD8jgIBo8x7fKFXCCVpKBfNHIjpxm2ZWm2JcG8OT7qthdNIze1IIfmjEbm54zY6u04Bmn1Z8AVi1F+wX1LUiXq64F+ZNpp4hosuudBASj7d+sEXCGQ3c6/IE02dmjABPXG/5AwGVKdfKF08NLMVxqj4h3eKmNE1v3EaJbtjc2b3RmDzZX8kIU+1fG/ktaq1Vjpgcojo226lWVF8xgxJRbaM3pTSK21xYcgeX1cVfDzrMaJLnxO4La4BNo0Hm7JnY1NFq1nsozNJ6h8Dq08aw/x1PfUJg1sauhAvha1VpTcWcm9joxXJqK5jlt3nTVSoNfd/pVxdWbbqN4etOaiu2Fd6syYT2EDnnin8VzNj7C2OyGNRUrWkhDMFdiJW2GDtCesZSXsLUHrUuoDtcfoIB9m7G8YZ3ihZnMrMPMqTdE68lrw+p1I8qrav0RsHCkwGzcaTmTacNrjTmUQBu4YXtUZVxS6CLZ8J7OQTA91d0C3KO0ayA7V2opGjN8QVGBVadewUqYtJAy8DII7d38ysxw2p9IJJ+grvWtz57vAwbHJ4DswIZoUS+pnvNaowu6Y82BGwy/tyI7dg743lgASV7b2NaMWVhYfeGhBnYmmw6KFHhboq2e1yMA9E6P49BwP9sB3k6w2lSdYlYmGb49ihOAx3rpG/66ePz+GmE3tA7z3Tj6zz12+fg9Bn/nTYzDsKuHyJ/gsFSUJa0yVJlZ8IModrmonP10Qj2dmohijThEfe1G66OV6s6hyBXQRbAlSy0ZhQXaf2IFtmJuiZAV2MWgZ3XYDhRMKjfw55g0PUu13ck8/MazjJkpdXx3eAcOHcYXk8DEl+CTAOP7BPjrKJQs17tekfQbOLy/ovdE4kHFCo8nFUDXKHC9toJ5bnxLez4/Huyfyl6Rtmfysi54ylUPokLD/apS0EGZaSGnjfGGsVpPJO+rjw2tpP7Sw9IMGu6Zvqff5/ufVgSGrg+Dk1EQousS4/gRDlwckLs8Tx6V55OHg3oNb1tGR74bto2HuBMcRPtMwI8I84dF/He6OyrgF7Yyn1bu7O7q3ACnLj7Z98XPe3h589iid9m13+PosfOjxx5I9EZfCd+oi9+vF742+V6dhG9xfvgWDyd8tw4M/bwwenwDw5npdxq//Pz45Q8lfr9a5xsPv3ww3/G1/1/14l9QSwcIZ42ssmIGAABMGwAAUEsBAhQAFAAICAgApY3hQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICACljeFAZ42ssmIGAABMGwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAPkGAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /> | ||
| + | |||
| + | Der Winkel <math>\angle {ABC}</math> besteht aus den Strahlen <math>BA^+</math> und <math>BC^+</math>. <math>\angle {ACB}</math> besteht aus den Strahlen <math>CA^+</math> und <math>CB^+</math>. Schneidet man nun diese Strahlen, so erhält man die Strecke <math>\overline {BC}</math> und den Punkt <math>A</math>.<br /> | ||
| + | Es müsste so heißen: Die Punkte der Schnittmenge '''des Inneren''' zweier Innenwinkel eines Dreieckes nennt man das Inneres des Dreiecks.--[[Benutzer:Andreas|Tutor Andreas]] 17:50, 1. Jul. 2012 (CEST) | ||
Aktuelle Version vom 8. Juli 2012, 23:39 Uhr
Inhaltsverzeichnis |
Die Aufgabe
Definieren Sie den Begriff Inneres eines Dreiecks.
Definitionsversuch Nummero6/Tchu Tcha Tcha:
Es sei ein Dreieck ABC. Die Schnittmenge des Inneren der Winkel 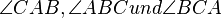 nennt man das "Innere eines Dreiecks".
nennt man das "Innere eines Dreiecks".
--Tchu Tcha Tcha 16:30, 20. Jun. 2012 (CEST)
Kommentar M.G.
Fast perfekt. Nur mit den bestimmten und unbestimmten Artikeln und dem Satzbau haut es teilweise noch nicht richtig hin. Ich nehme das mal auseinander:
- Es sei ein Dreieck
 .
.
- Hier kann man den unbestimmten Artikel "ein" wählen. Man muss es jedoch nicht. Es würde auch gehen: Gegeben sei das Dreieck
 . Das Dreieck steht für alle Dreiecke. Das Dreieck ist damit ein beliebiges Dreieck.
. Das Dreieck steht für alle Dreiecke. Das Dreieck ist damit ein beliebiges Dreieck.
- Was nicht so richtig zusammenpasst ist ihr Satzbau: Es sei ein Dreieck ... . Aus rein syntaktischer Sicht müsste das Wort Dreieck das Subjekt in ihrem Satz sein. (Satz im Sinne der deutschen Sprache und nicht als wahre Aussage der Mathematik.) Nach dem Subjekt Dreieck müsste ein Objekt kommen. Also etwas, was auf die Frage "Was sei ein Dreieck?" als Antwort dienen kann. Es folgt die Bezeichnung
 . Das passt so nicht ganz. Das wäre etwa dasselbe wie: Es sei ein Mensch Kevin. Das würde niemand sagen. Wir würden eher formulieren: Es sei ein Mensch namens Kevin. Hört sich auch blöd an. In dem Satz fehlt einfach was. Etwa sowas: Wir gehen davon aus, dass ein Mensch namens Kevin auch da ist. Mit unserem Dreieck wird es einfacher : Gegeben sei ein Dreieck
. Das passt so nicht ganz. Das wäre etwa dasselbe wie: Es sei ein Mensch Kevin. Das würde niemand sagen. Wir würden eher formulieren: Es sei ein Mensch namens Kevin. Hört sich auch blöd an. In dem Satz fehlt einfach was. Etwa sowas: Wir gehen davon aus, dass ein Mensch namens Kevin auch da ist. Mit unserem Dreieck wird es einfacher : Gegeben sei ein Dreieck  . Wenn wir auf das gegeben verzichten wollen, müssen wir umstellen. Es sei
. Wenn wir auf das gegeben verzichten wollen, müssen wir umstellen. Es sei  ein Dreieck. Wer oder was sei ein Dreieck?
ein Dreieck. Wer oder was sei ein Dreieck?  . Was sei
. Was sei  ? ein Dreieck. Analog: Es sei Kevin ein Mensch. Das macht Sinn. Unser Hund heißt z.B. Fritz. Seit den 90ger Jahren und den Back Street Boys muss man mit dem Namen Kevin vorsichtig sein. Manch einer behauptet, dass Kevin kein Name mehr ist, sondern eine Diagnose.
? ein Dreieck. Analog: Es sei Kevin ein Mensch. Das macht Sinn. Unser Hund heißt z.B. Fritz. Seit den 90ger Jahren und den Back Street Boys muss man mit dem Namen Kevin vorsichtig sein. Manch einer behauptet, dass Kevin kein Name mehr ist, sondern eine Diagnose.
- Hier kann man den unbestimmten Artikel "ein" wählen. Man muss es jedoch nicht. Es würde auch gehen: Gegeben sei das Dreieck
- Also korrekt wäre: Es sei
 ein Dreieck.
ein Dreieck.
- Also korrekt wäre: Es sei
- Die Schnittmenge des Inneren der Winkel
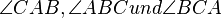 nennt man das "Innere eines Dreiecks".
nennt man das "Innere eines Dreiecks".
- Die Schnittmenge geht in Ordnung. Mathematisch korrekt ist auch, für die Generierung der Schnittmenge die Inneren der entsprechenden Winkel zu verwenden. Mit der Bezeichnung
 haben wir unser Dreieck jetzt aber festgelegt. Die Menge, die jetzt durch das Schneiden der Inneren der Innenwinkel des Dreiecks entsteht, ist jetzt definitiv nicht das Innere irgendeines Dreiecks, sondern ganz klar das Innere des Dreiecks
haben wir unser Dreieck jetzt aber festgelegt. Die Menge, die jetzt durch das Schneiden der Inneren der Innenwinkel des Dreiecks entsteht, ist jetzt definitiv nicht das Innere irgendeines Dreiecks, sondern ganz klar das Innere des Dreiecks  . Demzufolge muss es korrekt heißen:
. Demzufolge muss es korrekt heißen:
- Die Schnittmenge geht in Ordnung. Mathematisch korrekt ist auch, für die Generierung der Schnittmenge die Inneren der entsprechenden Winkel zu verwenden. Mit der Bezeichnung
Definition
(Inneres eines Dreiecks)
Es sei  ein Dreieck. Die Schnittmenge der Inneren der Winkel
ein Dreieck. Die Schnittmenge der Inneren der Winkel 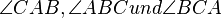 nennt man das "Innere des Dreiecks
nennt man das "Innere des Dreiecks  ".
".
--*m.g.* 18:35, 20. Jun. 2012 (CEST) Sprache ist ein mächtiges Werkzeug. Wir sollten nicht schludrig mit unserer Sprache umgehen. Je mehr wir sie vernachlässigen und ihren korrekten Gebrauch als nicht so wichtig ansehen, umso manipulierbarer werden wir.
Ich empfehle allen, die sich für Sprache und die Mechanismen interessieren, wie Sprache zur Manipulation von Menschen verwendet wird, das Buch LTI von Victor Klemperer.--*m.g.* 18:35, 20. Jun. 2012 (CEST)
Danke für ihren ausführlichen Kommentar!! --Tchu Tcha Tcha 19:11, 20. Jun. 2012 (CEST)
Noch mal drüber nachdenken
Keine Ursache, kehren wir ruhig zur Mathematik zurück.
- Brauchen Sie eigentlich alle drei Innenwinkel zur Definition des Inneren eines Dreiecks?
- Würde die Definition auch ohne die explizite Verwendung der Inneren der Winkel definieren können.
--*m.g.* 23:47, 20. Jun. 2012 (CEST)
1) Nein, stimmt. Anhand von 2 Innenwinkeln kann man das "Innere eines Dreiecks" definieren.
2) Es sei  ein Dreieck. Die Schnittmenge der drei Halbebenen
ein Dreieck. Die Schnittmenge der drei Halbebenen 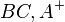 ,
, 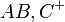 und
und 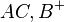 nennt man das "Innere des Dreiecks
nennt man das "Innere des Dreiecks  ".
".
--Tchu Tcha Tcha 07:06, 21. Jun. 2012 (CEST)
perfekt--*m.g.* 10:23, 21. Jun. 2012 (CEST)
Just noch ein sailA
Vorschlag 1
 sei ein Dreieck.
sei ein Dreieck.
Die Menge aller Punkte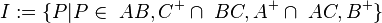
ist Inneres des Dreiecks.
--Just noch ein sailA 14:55, 25. Jun. 2012 (CEST)
Kopernikus
Vorschlag 1
Die Punkte der Schnittmenge zweier Innenwinkel eines Dreieckes nennt man Inneres des Dreiecks.
--Kopernikus 14:53, 25. Jun. 2012 (CEST)
Das stimmt so nicht. Was sind denn Winkel? Ein Winkel besteht aus zwei Strahlen. Bilde ich nun den Schnitt von zwei Innenwinkeln eines Dreiecks, so erhält man eine Seite des Dreiecks und einen Eckpunkt, der nicht zu dieser Seite gehört. Nicht aber das Inneredes Dreiecks. Hier eine Skizze als Verdeutlichung...
Der Winkel 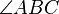 besteht aus den Strahlen
besteht aus den Strahlen 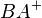 und
und 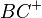 .
. 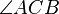 besteht aus den Strahlen
besteht aus den Strahlen 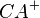 und
und 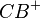 . Schneidet man nun diese Strahlen, so erhält man die Strecke
. Schneidet man nun diese Strahlen, so erhält man die Strecke  und den Punkt
und den Punkt  .
.
Es müsste so heißen: Die Punkte der Schnittmenge des Inneren zweier Innenwinkel eines Dreieckes nennt man das Inneres des Dreiecks.--Tutor Andreas 17:50, 1. Jul. 2012 (CEST)

