Lösung von Zusatzaufgabe 7.2P (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie: Jeder Winkel, der das Maß 90 hat ist ein rechter Winkel. Kategorie:Einführung_P“) |
|||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Jeder Winkel, der das Maß 90 hat ist ein rechter Winkel. | Beweisen Sie: Jeder Winkel, der das Maß 90 hat ist ein rechter Winkel. | ||
| + | Vorauss.: alpha= 90° | ||
| + | Behaupt.: alpha= rechter Winkel | ||
| + | |||
| + | 1) <math>\left| 90 \right| + \left| beta \right| = 180</math> (Nebenwinkel sind supplementär) | ||
| + | |||
| + | 2) <math>\left| beta \right| = 90 </math> (1., Rechnen in R+) | ||
| + | |||
| + | 3 <math>\left| alpha \right| = \left| beta \right| </math> (1., 2., Def.) | ||
| + | |||
| + | 4 ) alpha = rechter Winkel (3., Def. rechter Winkel: Winkel, dessen Nebenwinkel das gleiche Winkelmaß hat) | ||
| + | |||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 9. Juli 2012, 12:05 Uhr
Beweisen Sie: Jeder Winkel, der das Maß 90 hat ist ein rechter Winkel.
Vorauss.: alpha= 90° Behaupt.: alpha= rechter Winkel
1) 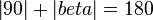 (Nebenwinkel sind supplementär)
(Nebenwinkel sind supplementär)
2) 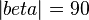 (1., Rechnen in R+)
(1., Rechnen in R+)
3 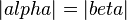 (1., 2., Def.)
(1., 2., Def.)
4 ) alpha = rechter Winkel (3., Def. rechter Winkel: Winkel, dessen Nebenwinkel das gleiche Winkelmaß hat)

