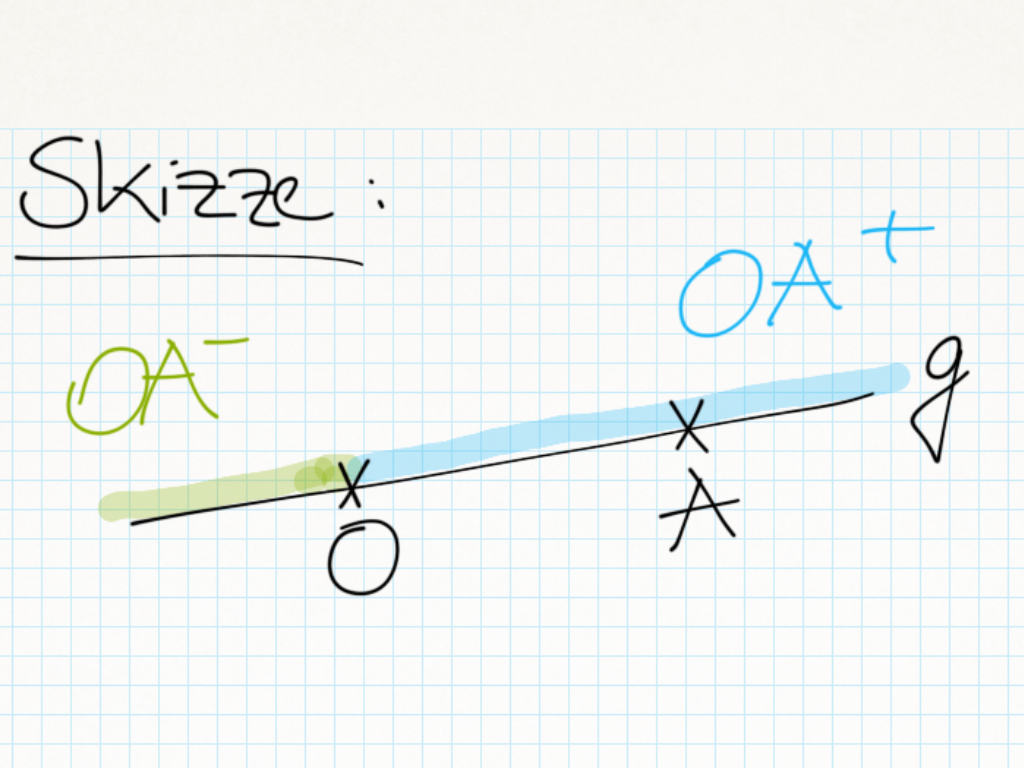Lösung von Zusatzaufgabe 7.3 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Datei:7.3.PNG<br />--~~~~“) |
|||
| (6 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | [[Datei:7.3.PNG]]<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 20:18, 12. Jun. 2012 (CEST) | + | [[Datei:7.3.PNG]]<br /> |
| + | Beweis folgt..<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 20:18, 12. Jun. 2012 (CEST) | ||
| + | |||
| + | |||
| + | Vorraussetzung: <math>\exists g; \exists A:A\in g;\exists O:O\in g; A\neq O</math> <br /> | ||
| + | Behauptung: <math>\ OA^{+} \cap \ OA^{-} = \left\{ {O} \right\}</math><br /> | ||
| + | |||
| + | Ich möchte zunächst zeigen welche Punkte zur Halbgeraden <math>\ OA^{+} bzw. OA^-</math> gehören:<br /> | ||
| + | Schritt 1:<math>\ OA^{+}:= \left\{ {P|\operatorname(Zw) (O, P, A) \vee \operatorname(Zw) (O, A, P) } \right\} \cup \left\{ {O,A} \right\}</math> <br /> | ||
| + | Schritt 2:<math>\ OA^{-} := \left\{ {P|\operatorname(Zw) (P, O, A) } \right\} \cup\left\{ {O} \right\}</math> <br /> | ||
| + | Schritt 1 und 2 jeweils aufgrund der Definition II.5 (Halbgerade, bzw. Strahl) <br /> | ||
| + | |||
| + | Schritt 3: <math>OA^+ \cap OA^-=\left\{ {0} \right\}</math> aufgrund von (1) und (2)<br /> | ||
| + | |||
| + | Ist dies schon ausreichend? Muss noch genau gezeigt werden, dass kein weiterer Punkt P in der Schnittmenge auftritt oder ist dies durch die Zwischenrelationen schon drin?<br />--[[Benutzer:Thommy|Thommy]] 16:53, 14. Jun. 2012 (CEST)<br /> | ||
| + | *Ich würde das ganze indirekt machen und annehmen, dass <math>OA^+ \cap OA^- = \lbrace O,X \rbrace</math> gilt und das dann zum Widerspruch führen. --[[Benutzer:Andreas|Tutor Andreas]] 12:05, 12. Jul. 2012 (CEST) | ||
Aktuelle Version vom 12. Juli 2012, 11:07 Uhr
Beweis folgt..
--Tchu Tcha Tcha 20:18, 12. Jun. 2012 (CEST)
Vorraussetzung: 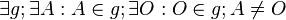
Behauptung: 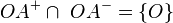
Ich möchte zunächst zeigen welche Punkte zur Halbgeraden 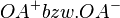 gehören:
gehören:
Schritt 1: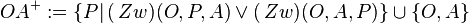
Schritt 2: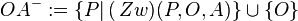
Schritt 1 und 2 jeweils aufgrund der Definition II.5 (Halbgerade, bzw. Strahl)
Schritt 3: 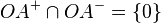 aufgrund von (1) und (2)
aufgrund von (1) und (2)
Ist dies schon ausreichend? Muss noch genau gezeigt werden, dass kein weiterer Punkt P in der Schnittmenge auftritt oder ist dies durch die Zwischenrelationen schon drin?
--Thommy 16:53, 14. Jun. 2012 (CEST)
- Ich würde das ganze indirekt machen und annehmen, dass
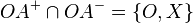 gilt und das dann zum Widerspruch führen. --Tutor Andreas 12:05, 12. Jul. 2012 (CEST)
gilt und das dann zum Widerspruch führen. --Tutor Andreas 12:05, 12. Jul. 2012 (CEST)