11.07.2012: Winkel und Lot: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „=Platz für Diskussionen und Inhaltsbesprechungen zur heutigen Übung= <br /> <br /> =={{Schrift_orange|HINWEIS:}}== Beachtet bitte die Informationen zur Vor…“)
 
(→‎Idee 1)
 
(5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 
=Platz für Diskussionen und Inhaltsbesprechungen zur heutigen Übung=
 
=Platz für Diskussionen und Inhaltsbesprechungen zur heutigen Übung=
−
 
+
Die Bilder des Lotbeweises sind online! [[Lösungsidee Übung Heckl Aufgabe 11.6 SoSe2012]]
  
 
<br />
 
<br />
Zeile 7: Zeile 7:
 
<br />
 
<br />
 
=={{Schrift_orange|HINWEIS:}}==
 
=={{Schrift_orange|HINWEIS:}}==
−
  Beachtet bitte die Informationen zur Vorbereitung auf die letzte Übung. Diese werden in der heutigen Übung von mir nochmal angesprochen und finden sich auch unter [[Organisatorisches]] wieder.
+
  Beachtet bitte die Informationen zur Vorbereitung auf die letzte Übung. <br />
 +
Diese werden in der heutigen Übung von mir nochmal angesprochen und finden sich auch unter [[Organisatorisches]] wieder.
 +
 
 +
<br />
 +
=Beweisideen einer Übungsteilnehmerin=
 +
==Idee 1==
 +
[[Bild:Aufgabe11_3.jpg]]<br />
 +
Aufgabe 11.3 - Version 1
 +
<br />
 +
===Kommentar zu Idee 1===
 +
Von der Grundidee kann man den Beweis so führen. Wir sollten dabei aber von der Skizze abstrahieren. In Schritt 4 argumentierst du glaube ich mit dem Stufenwinkelsatz (im Übrigen gibt es auch an geschnittenen Geraden Stufenwinkel, wenn sie nicht parallel sind); den gibt es so allerdings in der absoluten Geometrie nicht (nur die Umkehrung).<br />
 +
Allerdings weißt du, dass Schritt 3 gilt. Dass Schritt 4 gilt, weißt du eigentlich auch - nämlich aufgrund des schwachen Außenwinkelsatzes. Und dann hast du den Beweis direkt geführt. M. E. nach geht das so! --[[Benutzer:HecklF|Flo60]] 15:22, 15. Jul. 2012 (CEST)<br />
 +
 
 +
==Idee 2==
 +
[[Bild:P1140061.JPG]]<br />
 +
Aufgabe 11.3 - Version 2 = Übungsversion ?
 +
 
 +
===Kommentar zu Idee 2===
 +
Das passt so - ist genau die Beweisidee aus der Übung. Der einzige Unterschied, den wir in der Übung nicht hatten, ist die Differenz als Omega zu bezeichnen.<br />
 +
Man hätte folglich kürzer vorgehen können:
 +
 
 +
<br />
 +
Annahme: o. B. d. A. <math>|\alpha | + |\beta | \ge 180</math>
 +
<br />
 +
<br />
 +
Schritt 1 und 2 genau wie bei dir;<br />
 +
deinen Schritt 3 braucht man nicht unbedingt (deshalb wohl auch eingeklammert)<br />
 +
Schritt 4 reicht <math>|\alpha | \ < \ \delta</math> nach schwachem Außenwinkelsatz
 +
Nun folgt unmittelbar daraus: Wenn <math>\alpha</math> kleiner ist als <math>\delta</math> und <math>|\delta| \ + \ \beta = 180</math>, dann kann etwas kleineres als <math>\delta</math> - nämlich <math>\alpha</math> + <math>\beta</math> nicht gleich 180 sein und schon gar nicht größer.<br />
 +
<br />
 +
Schlussendlich stimmt dein Beweis und ist genau das, was ich beschrieben habe, nur ausführlicher - aber wir wollen ja nicht nach dem Motto: "In der kürze liegt die Würze" arbeiten, sondern um Verständnis für die Sache werben - aus diesem Grund: Toller Beweis :) --[[Benutzer:HecklF|Flo60]] 15:07, 15. Jul. 2012 (CEST)
 +
 
 +
=Dem größten Winkel liegt die längste Seite gegenüber=
 +
 
 +
==Teil 1: Konstruktion==
 +
<ggb_applet width="800" height="457"  version="4.0" ggbBase64="UEsDBBQACAAIAE2t6EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAE2t6EAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnbjuM2En2efAWhh32alkmRoqRZ9wTuBgY7wCQTbE+Cxb4sKIm2mZYlrSTfGvmpBPmOfNMWSUmWL+2+TNLJrDE9lMgSi1Wn6lTJHn+9WWRoJataFfmlQ1zsIJknRary2aWzbKYXofP126/GM1nMZFwJNC2qhWguHaYlVXrp4JhS4hNyEfpRcMGmjF6EkeQXHqUJn8ZkypPAQWhTqzd58a1YyLoUibxJ5nIhPhSJaIziedOUb0aj9XrtdqrcopqNZrPY3dSpg+CYeX3ptBdvYLu9h9bUiHsYk9G/vvlgt79Qed2IPJEO0iYs1duvXo3XKk+LNVqrtJmDwTT0HDSXajYHowLGHDTSUiV4pJRJo1ayhmcHt8boZlE6Rkzkev2VvUJZb4+DUrVSqazAQS71fS/0SBQFBPtc6ygqJfOmlSWtzlG323il5Npuq6+MRnioKYosFnpH9NNPyMMeRq/1QOzgwcC5XcJ2DlM7eHZgdvCtDLOPMyvKrAyzMow6aKVqFWfy0pmKrAYXqnxaAXz9fd1sM2nO007srCevwaZa3YEwxRAn1ucwj/Fr/cfhj+mF0b6RZKC1qZZPVNqpJJTzx+v0PstS2illETnW6fn32MnPKLWGP8pQf+BbUGX+mb8jjfScmYca7f3nKeTsRUwcj7pcGbfpgeq5lm3Dp5GLWicMjZAf6bgnyIfk4AGEuY9IBEPgIUgHRHzEfLglIeJ6DBANYIEhikKk5QhFJjv8EP5jgdmMIx8207MBJCUioIghnyJikoohSCVkEhOS1KMg4fvIh4e0euLpLShHjMMdDRGDM+qcDAgIUngQ7kG9hyhBVD9MAuRxxPV+hOlc56E+OmzpIY4RJ3pDSGtIaZvOIB8iqq3hrbtUXi6bPRcli7S7bIqyxwKkgZB2tGcJao8VX40zEcsMKsWNRhKhlch0RhhF0yJvUAeiZ+dmlSjnKqlvZNPAUzX6UazEB9HIzTuQrjvdRjYp8vq7qmiui2y5yGuEkiLD/ZmLjAyuvf7UcEMHC2y44A8W+OA6OKm3gBW0rCXoL6q6Exdp+l5L7KgBPPkxz7ZXlRS3ZaH2zRiPTNEZy2WSqVSJ/AcIVq1F+wXtapDmq64G+UHUnaSo0pttDSGMNv+WVQG+pS4Oo4BF9hNCYd22K0HksjCEvLAfnUCJ0LnHsctp4IPk/kQniZlVJ1c9LGIjdxbOKp3Og5v39VWR7aaM0deibJaV6RmAESttySSfZdIEhuFYKMjJbVxsblqKtnt92pZwh+0J4plxNgJC8Hw48KwdYzsaGX20XgobGWwkcBdiKu3XSeQZCTPGdjRSELP2aK2ppDOT4E6Nqm1347TJ0lGUjnhd3pe5aj50N41KbltTiX3g2+Uiln3c7O9Jfq89x6ODwBrfyiqXWRvHAOayWNY2LQchnspELeDWLrQuERqu7+EAdjaVs0p2B89MP2YdZlbxMEKPps1W76pi8T5ffYJYODjAeNSdclwnlSp1zKEYuP9W7qIqVbWA0pEOn9OJB6YnukSAexrtGkjJZTMvAOx3WcEBrRToBKaN+GIh8hTlpuS8zxvwHXCXs6NBAYSymQAssAvwydZcGhOKZdMJTOyZ2910MmdyAc0bakzsmvDvMZyY3TVYqIh/BG19MbXru2iA5T5Oda2c2SG2g8jKudCtY+vSTGxltedks+E3RXoCkRpt7KNoe+lcmIs729rb1lafWKfhHl/b2QMsIcCssUfu/M6YfcqVh/67eor/rp7lP+JZtjBjyxbPdqHIITlMiAHzljb5Silt3tozw0UJ2xm62ysdnfO5S4zzfy/fn3PZ9bNcNqTOP91dvgsdgvaX5+q3sT8gWLPtrMgPwvXKZv01DF6b5nuBC5SaQc0iVkxYsRgG6DCSh4LaKuww6LfaLz4NNEO38MpXmwrZtLXQXPxDpak0jfDoPLwDhw7xhVc4W0AxO4ExeQrG9wdiLWf6rj+LeFYonj/qswnwwgaTpcAoiIYf3wZZ4HqYDKbDw+7g8QDJ/+b2kdqWbLUoM5Wopo+qTMd/X4QgX47r8q2UpW6IPuafKpHX+psWKzOo949EIn5xJD5Op7VsjOP12+121/U/BNQOJ8sDd23R+n/BIvlLZUXXF5gSdTfc60vw9D6vX6sqyeQBrV9bvr464vP0PGdDd6mSHpT0AdDuod39N5Jn43USi1099U+DoWYyX8FR4X0VoQ1uv83d4q4P6WY2pI8D0k7dkUHNhXpeqQ2adPKTTmri6Th0PZ/ukSaa0FbFhPVZPPE7Cj4ZKfprBDVVyXmA72vaU4txfNxs/k2URf13u/ykxrN98EXb9wFnUsuA/LGU6WMWhTjwQ0JC0vIncWkQ8YgzSmHKg5L3B/RSNy27neylOi8ewiLPQ3HImPJPTb4BWZ7yqIaJun7kQ+vgMRKC+0nAjKdDlxFOWOgxWCARDr5YZjVf3pzH2LTD10dQ//brf8h5tM3XAz2WRt785iGyZQeEG/IoDMMA8zDwMHj+oS74nvdC3H7/g73PbYKfh6Kokl2++d0bU5YV63/KaSY3xs2fg0lf7Awa96Uf+Nh7Iibeg5jwl8dkwJehTcToC0fs+K3zt1+ehNQvhzgR16OcUuZHHqdARSF7Hk64RemYTh+NUftS/+Vh1DLd5F6O+/lJGP18nEs+pozp34QJjijlL4zRXwGF0fDbXPNLSfuz/9v/AVBLBwhJg4JF6gcAAJMgAABQSwECFAAUAAgACABNrehA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAE2t6EBJg4JF6gcAAJMgAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAgQgAAAAA" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
 +
 
 +
 
 +
==Teil 2: Der Beweis==
 +
<ggb_applet width="1200" height="500"  version="4.0" ggbBase64="UEsDBBQACAAIAO+s6EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAO+s6EAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vxbb+PGFX5OfsVUDRZbYC3PnUPHTiA7CLqoc0F2mwTFAgFFjiSuKVIhKVs2/F/60j+QoI99y3t+U8/MkBJ1sWxaVrqud63hDA/ncr5zvnOGo93jz2fjBF3qvIiz9KRDuriDdBpmUZwOTzrTcnCgOp9/9vHxUGdD3c8DNMjycVCedLiRjKOTDu4zRgQhB0r43gEfcHagfC0PKGOhHPTJQIZeB6FZER+l2dfBWBeTINRvwpEeB+dZGJR24FFZTo4OD6+urrr1UN0sHx4Oh/3urIg6CKaZFied6uIIult66IpZcYoxOfzxq3PX/UGcFmWQhrqDzBKm8Wcff3R8FadRdoWu4qgcwYKZoh000vFwBIvyOO+gQyM1AY1MdFjGl7qAZxtVu+hyPOlYsSA19z9yVyiZr6eDovgyjnQOCuoyIaiixPc9goU0Y2R5rNOykiXVmId1b8eXsb5y3ZorOyI8VGZZ0g9Mj+j2FlFMMXplCuIKCoWU7hZ2bZi5grqCu0I4Ge4e506UOxnuZDjroMu4iPuJPukMgqQAFcbpIAf45vWivE60nU/VsFg9eQVrKuIbEGYY7MTpHNoxfmV+Jfxyc+NweZGkMWqZT1sOWg9JmJQPH5PutFJWD8p9sj4mFXesU24Z1C38QQsVDd3CUPav/V0bkW1b5uqIrr7bgJL/IUs8Pqx95bhyD1SMjGxlPqUeF8ZhmI+Eb+yeIAHOIT0wc4GID4VHEbgDIgJxAVWikDSlh5gHNzhiSCEjRxiy3iEUfHDPdiaRgM5MqwdOiQgMxJFgiFin4ghcCVnHBCelDCSEQAIeMsMTarpgEnEJNaYQhzkan/QICDJ4EOowPEWMIGYeJh6iEknTH+HG16UyU4cuKZIYSWI6BLcGl3buDPIKMbMaWakrTifTcklF4TiqL8tsMscCpIGQFrTnCGqJFT86ToK+TiBSvDFIInQZJMYj7ECDLC1RDSJ1bcM8mIzisHijyxKeKtD74DI4D0o9+xKki3psKxtmafFtnpVnWTIdpwVCYZbg+ZyzhDSu6XzWUGGNG7x5QzRuyMa1t3HcDO6gaaFh/CwvavEgil4biQU1gCa/SZPr01wHF5MsXl7G8aENOsd6GiZxFAfp92CsZhSjF7SIQYav6hgkPL+eSZZHb64LMGE0+4fOM9At62Lle9x3PwoC63V1x/O7XCnwC/djHCgMjO9J3JXMEyC53FBLYu6G05dzWIKZXqxwmBt3blReF6dZsmiyiz4LJuU0tzkDMGJuVtJLh4m2hmE5FgJyeNHPZm8qinZ9vb2eQA27GfSHVtkICIEKmPCwKvuutDJmanMpbGWwlcC1icXR/D7xqZWwZd+VVgps1k2tWiqpl0lwPUxcuOymUzlLTVHG4k14n6ZxeV5Xyji8qJZK3ANfT8d9Pbeb5T7JU/V5fLhiWMcXOk91UtkxgDnNpoVzy4aJRzqMx1B1NyqVBAauv8MEXGukh7muJ57YfMwpzN7FTQtda7ZdfZln49fp5VuwhZUJHB/WszwuwjyeGJtDfeD+C72wqiguAggdUfM543iw9NCECFBPaVQDLjktRxmA/WWSSUArAjqBZis+HgdphFIbcl6nJegOuKuzoMEACGXWA1igF+CTa3tpl5BNy1qg5+Zc9WacOdFjSN5QaW3Xmv8cw57t3YCFsv57GG0eTN39hTXAYqLYrsRSSCU8qobvv58bsQmkQ1f0XREkk1Fg8spK30lwrfMlBOxoX2XRBrgKNHOPouuTzoG9uHF5v8t7zXKMjy6RuWtdARqsz2liTdffWp1s0vOqck/bKPf06ZVLqOMZW1Y882j9Bim4lRu11BPnthOtnce7BcHFBLqzRLkUdGpkZJdYZJ4KmG36PHt6fTYZ+X+uS9GFxMMok3bNJm8PZp5cD7N0xdBPHZmcQUEr9lgyeWDqBEIhcWKBE+tDAYlLeJ87uAFrgOZdLce0EnKsC9hJFjbwllWItRd/jaNI2/z6cDv2yxnRw8CHbaML2phvMADSxgDuNuFCD01tPtHg6Y14+zoeTboHzgwd7fqe3/wRzjy9LsWk0axW05WHQ6t/Tt0jhcsh4vEkicO4nNtjYjxnHhVBLeuJwoXWE5OhfZO+zYO0MK9+nEwjAXkgTP0PC6ZvBoNClxYVsxe/XuxR7kNxAaKjl5sqiv6/ABV+WEBt86c6i7Ex86bZ13OAYTmWnMV5mOiVUHLmYsTpWgyJtscJQCYO54hF9yB6L9UPt8d5/HgwNwK1CPBiM1LxUKeXMDPYlyM0w9Vb62tcZ011y4zMjYRUTTekkQRAgpHHM9Sr5Xu1VI8aI+1SwZa4GPVYNUSPz/2/J2pm32hG5nVJPIjD7ejftTmJnAH01/PmF8EkKz51t1vl0NWDuzn5Bot49DalQcXMEat8KBMLzH2FPaEIUaSiZdJlni99yRmDJgphdg+Z35uKNDdmfrWKVzHT23FaJWK9q9uO9+a2DQ7epG6DIesKX0AuQzlRgA3xuIVBdTmRhCvK4QbxsfdsCdu+3tpuADazP1uzg9///RPZbgr2BcocaCtv+oCZTWsgukr6SikPS+VRDJq/L6G/z6U3WAvB1eszTHfN5x8HcZCHC08V9c4wSbKr7/Qg0TOLwS6AzQOsheouxwUAaEvA6L2AyQ8MsAYNK+fC/jOHc33r/fuvrWD8dRVE0qVMMsaFTyUDElN8VxDvfIVC8DpLPxjA6rXH8wOwItDendT5SysAf1n3QoEZ5+YwnmCfMfkhAfghQKRnkxyGMausFPBWz0rIyOHGSefFz9Os/PQT9EOco3foKksSncJFX1/puNDpEbp9Z9d6i14My0+h1tclVE5cbd7cv0WfuK7s8MsQljBeZ3nwB+dBe0h14uI8eKt/XNZYdbpZ6DwezA+z7bkW7tTpSPV8UQZ5ad+HI+OafldIJoTC1KceZcSzjiq6ElJYAlUqOKRKSy8r74eHrsBzavEAYKJpHo6g/MF8EaWY5NNw9Kc2qqe7pqCD54ILgTyWKsKpFBj2epDSVsAQzHxCIZdlkK9K0Q4YtgJML02D0VgfASTWG5L23sB23sz/RJ4TKJ4nCSROEnYRsJOwoPCuxD40Ug6RmPtC3gnKkir7WZboYPHyfLAaHBqqe0g82F1/i4gtiTv1kWqbesNgYuG0bc7JwbH1Ubt1D9d3Ey1XvmdfX1eLyWcfqpfax9opZbQXlTyhr21QCtv+nqSplL+5k/ML2/JFrmMdXqDe6VlLy9mLku45RXycityL4cX3PR7qT0U4yuOyRGTdfjYyPF9l+H6ZB0ObFV1m5vP27PQWimA6sJXe7RGqtpltWJ9/uK9wn57zOWdCUU9Kzny/2sqwLlA+UD31PelhodjjOP/9ftx8fxZMaZuIMMx/+08aTdPhg+1XbM5QwFZfNvP1v7yClt4szsbWsM3nOWxOgqSNEYtdjfj9czJiiTEk8oQITD0lq68hcEU8jypmN6HCb5dNyhWsbt9FOimDn2idSVbbrRaQyF0huXhGkAgqsTnQIZ7gQC/V12x8yYXwIbu0n3fnkhsh8VYgeUmsp5zr8Tgw+y7yyu6+0gudBJFTXxFYN/rkxZ8Jhie+0+EotfEituHiuzbwebvClzwb+GhXeYoxxZX0YYdWH9pDWJDcJ5wLLKnyuPe4uHCxl7iQ7i8uMLz15d6WzIa1zIyTvajmyXijoRrsjp4Y81qoZhEyNyhmo8+rFZ+vWJigd7DUYV2lbfxYfbhHfXugYewLrgSXEvwW136saB0rqc8Ib0fD/mYaPg2KuLiy7FsE5U0bRPxdEXky3/8jmJVQ5lEPSykUp/UxulIKN/7c/eprK32M90IfT5YJrtMHJAmPZFbaklnTvajmyahgg2rq866WzLpBMZuPGfBahlsfJ7j8tmJas6GephF8Ftk4LqFck3SZcKtjBryry2fPxuU3k7D5qpTwILvyzNEY7MB93PJ9N1k9KHpJLRG/ZFCAm1wF4Uibo6Pe9Ld/6nRBza/m+bD9Hgbo9jIuf/uXgda9LDmp3pnUwLuqAdtdtQG6xYHSZqAnzwno5qZH1ThL2O4oLikB2ueeVI/j9mwvBPZke5ImgbmVM8Ueye28JbdP9qKaJ2OYpmrcESSn4lHcvkExm6lh9ZCycSYJ/nwzNbTwfZYH0wJmdmO6buPTO59UPhuf9rvc94RPKfex+R5R9Z1J0vU4xsz8BwOeIEypO1Pow+Y/o7P/RLX6/xY++y9QSwcIAGqecGIMAAAMQgAAUEsBAhQAFAAIAAgA76zoQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACADvrOhAAGqecGIMAAAMQgAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAPkMAAAAAA==" showResetIcon = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
 +
 
 
=Zurück zur Übersichtsseite=
 
=Zurück zur Übersichtsseite=
 
[[WIKI-Übung-Heckl]]
 
[[WIKI-Übung-Heckl]]
  
 
[[Kategorie: WIKI-Übung-Heckl]]
 
[[Kategorie: WIKI-Übung-Heckl]]

Aktuelle Version vom 15. Juli 2012, 14:22 Uhr

Inhaltsverzeichnis

Platz für Diskussionen und Inhaltsbesprechungen zur heutigen Übung

Die Bilder des Lotbeweises sind online! Lösungsidee Übung Heckl Aufgabe 11.6 SoSe2012




HINWEIS:

Beachtet bitte die Informationen zur Vorbereitung auf die letzte Übung. 

Diese werden in der heutigen Übung von mir nochmal angesprochen und finden sich auch unter Organisatorisches wieder.


Beweisideen einer Übungsteilnehmerin

Idee 1

Aufgabe11 3.jpg
Aufgabe 11.3 - Version 1

Kommentar zu Idee 1

Von der Grundidee kann man den Beweis so führen. Wir sollten dabei aber von der Skizze abstrahieren. In Schritt 4 argumentierst du glaube ich mit dem Stufenwinkelsatz (im Übrigen gibt es auch an geschnittenen Geraden Stufenwinkel, wenn sie nicht parallel sind); den gibt es so allerdings in der absoluten Geometrie nicht (nur die Umkehrung).
Allerdings weißt du, dass Schritt 3 gilt. Dass Schritt 4 gilt, weißt du eigentlich auch - nämlich aufgrund des schwachen Außenwinkelsatzes. Und dann hast du den Beweis direkt geführt. M. E. nach geht das so! --Flo60 15:22, 15. Jul. 2012 (CEST)

Idee 2

P1140061.JPG
Aufgabe 11.3 - Version 2 = Übungsversion ?

Kommentar zu Idee 2

Das passt so - ist genau die Beweisidee aus der Übung. Der einzige Unterschied, den wir in der Übung nicht hatten, ist die Differenz als Omega zu bezeichnen.
Man hätte folglich kürzer vorgehen können:


Annahme: o. B. d. A. 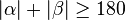|\alpha | + |\beta | \ge 180

Schritt 1 und 2 genau wie bei dir;
deinen Schritt 3 braucht man nicht unbedingt (deshalb wohl auch eingeklammert)
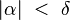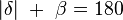Schritt 4 reicht |\alpha | \ < \ \delta nach schwachem Außenwinkelsatz Nun folgt unmittelbar daraus: Wenn \alpha kleiner ist als \delta und |\delta| \ + \ \beta = 180, dann kann etwas kleineres als \delta - nämlich \alpha + \beta nicht gleich 180 sein und schon gar nicht größer.

Schlussendlich stimmt dein Beweis und ist genau das, was ich beschrieben habe, nur ausführlicher - aber wir wollen ja nicht nach dem Motto: "In der kürze liegt die Würze" arbeiten, sondern um Verständnis für die Sache werben - aus diesem Grund: Toller Beweis :) --Flo60 15:07, 15. Jul. 2012 (CEST)

Dem größten Winkel liegt die längste Seite gegenüber

Teil 1: Konstruktion


Teil 2: Der Beweis

Zurück zur Übersichtsseite

WIKI-Übung-Heckl

Von „http://geometrie.zum.de/index.php?title=11.07.2012:_Winkel_und_Lot&oldid=16928“