Sehnenvierecke und der Satz über die gegenüberliegenden Winkel im Sehnenviereck: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Begriff des Sehnenvierecks) |
AnnaP. (Diskussion | Beiträge) (→Die Satzfindung) |
||
| (18 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
===== Definition XV.1: (Kreissehne) ===== | ===== Definition XV.1: (Kreissehne) ===== | ||
:: Es sei <math>\ k</math> ein Kreis. Die Strecke <math>\ \overline{AB}</math> ist eine Sehen des Kreises <math>\ k : \Leftrightarrow ... </math>. | :: Es sei <math>\ k</math> ein Kreis. Die Strecke <math>\ \overline{AB}</math> ist eine Sehen des Kreises <math>\ k : \Leftrightarrow ... </math>. | ||
| + | wenn die Endpunkte der Strecke <math>\ \overline{AB}</math> auf dem Kreis liegen. | ||
| + | --[[Benutzer:Nicola|Nicola]] 19:22, 25. Jul. 2010 (UTC) | ||
| + | |||
===== Definition XV.2: (die Durchmesser eines Kreises) ===== | ===== Definition XV.2: (die Durchmesser eines Kreises) ===== | ||
| − | :: | + | :: Ist eine Sehne, die durch den Mittelpunkt zur Teilmenge hat. |
| + | --[[Benutzer:Nicola|Nicola]] 19:22, 25. Jul. 2010 (UTC)<br /> | ||
| + | Vorschlag--[[Benutzer:TimoRR|TimoRR]] 15:56, 26. Jul. 2010 (UTC): Der Durchmesser eines Kreises ist eine Sehne von k, die durch den Mittelpunkt von k geht. | ||
===== Definition XV.3: (Radien eines Kreises) ===== | ===== Definition XV.3: (Radien eines Kreises) ===== | ||
:: Das können Sie selbst. Hinweis: Jeder Kreis hat unendlich viele Radien. | :: Das können Sie selbst. Hinweis: Jeder Kreis hat unendlich viele Radien. | ||
| + | :: Der Radius ist die Strecke <math>\ \overline{MP}</math>, wenn M Mittelpunkt des Kreises k ist und P ein beliebiger Punkt von k. --[[Benutzer:Nicola|Nicola]] 19:22, 25. Jul. 2010 (UTC) | ||
| + | |||
| + | ===== Definition XV.4: (Sehnenviereck) ===== | ||
| + | :: Ein Viereck, dessen Eckpunkte auf demselben Kreis k liegen. | ||
| + | :: Ein Viereck, dessen Seiten Sehnen desselben Kreises k sind. | ||
| + | --[[Benutzer:Nicola|Nicola]] 19:22, 25. Jul. 2010 (UTC) | ||
| − | |||
| − | |||
== Der Satz über die gegenüberliegenden Winkel im Sehnenviereck == | == Der Satz über die gegenüberliegenden Winkel im Sehnenviereck == | ||
=== Die Satzfindung === | === Die Satzfindung === | ||
==== sehr speziell: Quadrate ==== | ==== sehr speziell: Quadrate ==== | ||
| − | Jedes Quadrat hat einen Umkreis. | + | Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.<br /><br /> |
[[Bild:Quadrat_als_Sehnenviereck.png]] | [[Bild:Quadrat_als_Sehnenviereck.png]] | ||
| + | |||
| + | ==== weniger speziell, aber immer noch ziemlich speziell: Rechtecke ==== | ||
| + | Jedes Rechteck ist ein Sehnenviereck. | ||
| + | <ggb_applet width="419" height="444" version="3.2" ggbBase64="UEsDBBQACAAIAEKv9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VrLcts2FF03X8HhXjQeJEjMSMlIdheZSetMnWbRTYYiIQk1RaokZEv+qyb5jn5TLwBST0s2/Yhjz3ggXoDAxTn3XDyk7rvFNHOuRFnJIu+52EOuI/KkSGU+7rlzNepE7ru3b7pjUYzFsIydUVFOY9VzqUdcbZ/Lt29+6VaT4tqJM9PksxTXPXcUZ5VwnWpWijitJkKoLXs8X8hMxuXyfPi3SFS1rrCdvM9ncxhFlXOwJdP0g6yaxxMz4CyT6kxeyVSUTlYkPZcF4Dp8+ixKJZM467k+shbSc8lOJZiorp0UpbwpcqWbrzsfgcVxKnkj4E2kbd0TM9GumCeZTGWc68kYP6CR41zLVE1gQMyhSyHHE6VH57a3pCjK9GJZKTF1Fn+Jsui5Hcy8wA8JxZwGiIUsCF1naes493yMQ59w5gc0wBhABI/BFco9gpgfhhjmSjAK4J2DVWZocXUhlAIqKydeiDXI41KmWw/vq0GRrU2zQubqNJ6peWnigNamC7XUowFwpZ5kPx9norYRoGkiksthsbgwwGFqu/60nJlXjEPD8WmRFaVTakrA/3FdDm1p2mhPV62QaYNMi7oP3emqHnNiWphyaEvTKpO5da2eOW5mjVEzjKwcbYDOdfiuJp/FQwHh4DrzXKoPzQOEzWU9VWxf+H0+HYJuNgNn1Sd+qj67Jzsh170UZS4yG1g5cDsv5pVzpQPYjmUcSUUip/BoK2pIYk3Xn+CAtaZiXIrGcas6C5ipRZvBu2PunjROaB8q8DVRkD5gPkrPRatbgbJ67tQbe66TxkpbtXwyMRWgLWViwoTUCpvf3FUiKUxOaNRf169Rhupb48NEUpzNJjFYvHoCWbyEDLE5JdPf+WhUCeUsQIug2SWEON2o/a1It2GIc4DTzBFkPNPda8JmQqR1zlR1lDszGNBoZoMNA2KlB2O6LYzWofrDjX3ZtLH60tnEjEtr8i1gd0A3+IL3wduOvA1vngK+ZwOI1wChtvgkxXQa56mTx1MY51SWSSYMKFKvJE6MdIQ5MbZoWSDmqqlKbHd1J3twQ5TLZIVl4m4nGDUBHeeiqkwWVJv57nA434MQ9HA67uUcLFQivwLXirJynAWqmVqiBv7GsgDUOsa0xLXpBm9wA8yXcuH0m/b9plVfL73M41t/DOy0HqLvQ89GFP1A7ykaz/7JrfeVzY4QSIkcyeQ46R+NKLY5T/ao7h+neltZ/QclJUzs0mbKhycm4hspkOhHCI94lDKKCUJRGFEW4sAmqsDDlPtgCaA+IBF7jCw/QFjuENS3olz0Yenc4yo+zpWO8hUV8QNV2TpPPkKWa7hRnedwnef2YW6h4x21yClsjhOpjnPxPlew0wAI9hRjCImh0OptprjByqCNggYPUhDzDeC6GNqitXyIBZji+xHCPcYoi0LOMcGMguiePvzPS9gWjYs8zm4RwqDBfRfuYQsRDF+VCDp4Z7XfJ+G5VXCUkv4hStIWlKSvm5Jb1oUXzkzDw5nptE1mOv2xmal97kFexFAABh+q/RD7+DHJ5w5U08OonrVB9eyl8n2HUAsbDu+H+qEdzy7sAXkM7B+LbAn55fbMMrCgn0JBa5y3kIcjfyaSS1znoS/Yth+aD/BGYj7AHjq1Z5pjJFk3GhpWPT/fUQYH1JAa4L30hNso5fApuBJj/bTeAn55ofk8ehsYepSENAx4RHxKWGC3GTT0WBBxwlFEw9BH/hOlXhNjmT4MrJICHCD2b5EuhZjp67vz/FMZ55W++rVtNm6n7knN8NVR0/E9EkachRTp/yDEW+uijz19dYt8HrIo4E+1Kr4ANcmrowZ7GCNCKCI+IwEOWPBrp8netyupwzygEJ4jjCKCOX69dKWvjq5dIaFgS0kd7nEeIkRCRDkKafBUZ99nIWd7dTffgOys7Wd2te7btXqwt6j/9+/xpdpc0694gtb6ffBnXuPreyEmNIp4hGjkM34X08cuzjHaPzscX5w3NlzY3pwf2G+1kVhcJusNVdQYs6y4/kOMMrEwMO/w1o6U3Q3XHilfW5Hy9aclpT48YP4KSKmVcnpQKd9akfJtlxTsQbIJOZyoWMh9SEHs5Wjh9eHk9q+Zfi5earGcHRTL91a8fL+Tl+jlchirebn9mvBH8nKy+V2q+clB/ZuLt/8DUEsHCFxRBbNRBgAApSEAAFBLAQIUABQACAAIAEKv9TxcUQWzUQYAAKUhAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAiwYAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | ==== noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze ==== | ||
| + | Jedes gleichschenklige Trapez ist ein Sehnenviereck. | ||
| + | |||
| + | <ggb_applet width="419" height="411" version="3.2" ggbBase64="UEsDBBQACAAIAJGx9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VrbbtvGFn1uv4LgQ9GiNT1XcohaKWT7JUDcFHVOcNALCoocSVNTpEqOHMkH56OK/sf5prNnhpQlSpYtxU7sPITi3Getvfbs2ebJD/NJ7l3LqlZl0fNxgHxPFmmZqWLU82d6eCT8H159eTKS5UgOqsQbltUk0T2fBsQ35TP16ssvTupx+cFLctvkvZIfev4wyWvpe/W0kklWj6XUa+XJbK5ylVSLt4M/Zarr2wo3yOtiOoNZdDWDsnSSvVF1+3psJ5zmSp+ra5XJysvLtOeHHJYOv97LSqs0yXs+Q66E9HzSqYQiamrHZaVuykKb5reDD6HE82p1I6EnMmUnx3ajJ3KW5ipTSWE2Y9cBjTzvg8r0GCbEMQwp1WiszeyxGy0tyyq7XNRaTrz5L7Iqe/4RDgPOIkJxTDkKo5BHvrdwdXEcMIwjRuKQccoxBhBhxbAUGgcEhSyKMOyVYMShz51Vdmp5fSm1BiprL5nLW5BHlcrWXl7Xp2V+WzQtVaHPkqmeVdYOaFN0qRdmNgCuMpvsF6NcNmUEaBrL9GpQzi8tcJi6od8tpraLXdBgdFbmZeVVhhJY/6h5DtzTtjErXbZCtg2yLZoxzKDLehwT28I+B+5pW+WqcEtrdo7bXWPUTqNqzxTA4MZ8l5vPk4EEc/C9WaH0m/YFzOaq2Sp2HX6cTQagm1XDWY6JH2vMk+OOyZ1cyaqQuTOsAridlbPauzYG7OayC8lkqibw6ipwszpD179gAa40k6NKtgt3qnOA2Vq0aryd4pPjdhFmDTWsNdXgPmA/2uzFqFuDsnr+JBgFvpcl2pQa+eRyIkFb2tqENaklNhf+0pGU1ie06m/qb1GG6q32YS0pyafjBEqCZgN5sgAPsbolO97b4bCW2puDFkGzCzBxulJ7UWbrMCQFwGn3CDKemuENYVMps8Zn6sbKvSlMaDWzwoYFsTaThaYtzHZEzY8b19m2cfoy3sTOSxvyHWD3QHf6B94Eb93yVlbzGPA9GUBxAxDaF5+0nEySIvOKZALznKkqzaUFRZmTxEuQsTAvwQ4tB8RMt1WpG64ZZANusHKVLrFM/XUHo8eg40LWtfWCetXf3W3ODyAEHU7HgxYHB5UsrmFpZVV73hw1TC1QC39bMgfUjmzRAjdFN3iFG2C+UnOv37bvt6365ugNg3jtXwjltJmiz2BkK4o+NzFFu7K/Crf62nlHMKRUDVW6m/SfrCjWOU83qO7vpnpdWf2DnBIm7mizz8MdEyNWCoR9CuHRAPOY4AhHIsaYsZA3OsQQgggSCYEQJSI0Wzlcl2/ALjsM9Z0q5304OzfISnaTZcx8yUVyoCz3dpQfoctbvFHj6HDj6I62Ib2HljuKURMIkFOld9PxutAQbQAKG6qxnCTwMApud7lCzOk+Kjo9SEUhs5ibx8A99pYQcRhT/DBORCAYigQREEELwTl9Cgm8rSA2GpVFkm8Rw2kLfBfvwR5CGLwoIRzhzpG/ycJTy2AnJf27KMn2oCR72ZRsORyempMtTFzsOinkHmzIF8VG96RYRklPiP6lHJny7VI43QB/uBv8uhltidzzD6A34edBKDAPechACBFGYXtsCy5izmLKEBIIi0fixuKbm4BteUhDkLd507+ScmpSLG+Ld1VS1CY959qsZBAOcXuN2IYbXI/2ENroRQntaAvFq06QBUjENKaCUxSSkD25Cu8Kz0Z3cXPmrrYPjcvODs4bHByb7YAfx9Tgj4kQcPojhl34xQKIuwhEAgwTKhiPHRkkIEZtArOQhhHlh4Ri56rWSZHeYfpnW/IEycD0yC7OdsNczCayWskY3HYz48HSZu0Cu7Fl+HA7xxspovm0Auszd8Fm3ndyrmFSD2p6/ld/zUr9/W/ltayMzf7HvXvfel//CGj8evH7N8vfsHX75pr81/vtO69n/lt2ud2Qd7yxew2z+p0lfFaJq/pN8k7+e90vwnp0UmmbNHAAXajM2s+vF995BoHdKbgux+Mutyhg97q2+5OaG4w/YNvLfO/hqYFdoskT3ZWM0YoVzdHX42/crfFi0zt9lUzL+vu9PFTT5fl6KeTyJEeYRgE3hTTixlER/nh+asvx3AJzx0Gg9jik1aMc0vtZ8scHw4IGDI4FuChC8IWpyZUB3JHAAY1iSmgMJDDRKuazpVCUEwPekkI530cI5582hbJLAEHMREw4pjFjEPGyyAmABSSEF4oxJwhTzD4mSfIwVLclpu45mTvu5fmgCn05RhETIeI8xvFToPpTmS8g3u9get6EOw5Tk4GiTZZ8Ddj3CoZNrxo/n1mHD+1T+wN6DOwPBsHO/UGoW0aL8nLkp7sVYpPLA844PvhQRbvDge4dN/vjM+3no12rCDAimMURwRCa0pi0tx+ORRzDrYjgEAz1Od9zd1OTvjhqwA0wjENwDHBJQCxEy6gjIEBWTBA44wiFjDVRRxxgwVkYQVtGEYvDl8vW4MWx1QppWz7hxlS/oIzRbm6SF8fNQ4UErNj0HqZBxCHOgaCSIMIivPF50XNia/24t59nbT/s++1h3z3l//f37rPbfkO0JA5ady69OBAUPI9gMeZg3pyL+8jfdXHAaN9L8Mqfz4lwN4Xtfz7f52aQVOltjCXawjwvP/wsh7mcW6A7zB1Ey9mdtPyzFy3/dGlhQQyeBkyfweU0BnY+Gyu8Edz2z60+JSvHq9+u2U88m29cX/0fUEsHCCkjpU3sBwAAFSsAAFBLAQIUABQACAAIAJGx9TwpI6VN7AcAABUrAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAJggAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | ==== allgemeines Sehnenviereck ==== | ||
| + | Ausgangslage: <math>\ \overline{ABCD}</math> ist ein gleichschenkliges Trapez. | ||
| + | |||
| + | Arbeitsauftrag: Bewegen Sie den Punkt <math>\ C</math> auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von <math>\ \gamma</math>? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck? | ||
| + | |||
| + | |||
| + | <ggb_applet width="419" height="411" version="3.2" ggbBase64="UEsDBBQACAAIAJKz9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vpbb+M2Fn7e/gpBD0WLrRXeSaHxFE7yMsCkU2xmB4ttF4Us0bY2suRKcsaeRX9UL79jf9MekpLje2LnMhNg52FkkxR5+H3nOzw88el3s3Hm3eiySou86+MA+Z7O4yJJ82HXn9aDjvK/e/XF6VAXQ90vI29QlOOo7vo0IL5pn6avvvjLaTUqPnhRZoe8T/WHrj+Iskr7XjUpdZRUI63rlfZoOkuzNCrnb/v/1nFd3Xa4SV7nkymsUpdTaIvHyZu0ar+e2AUnWVpfpDdpoksvK+KuLziYDp/e67JO4yjr+gy5FtL1yVonNFHTOyrK9GOR12b47eQDaPG8Kv2o4U1k2k5P7EZP9TTO0iSNcrMZawcM8rwPaVKPYEEcwpQ6HY5qs3roZouLokyu5lWtx97sn7osun4Hi4AzSSgOKUdCCi59b+76wjBgGEtGQsE45RgDiGAxmELDgCDBpMSwV4IRh3d2dtml9c2VrmugsvKimb4FeVimycqX19VZkd02TYo0r8+jST0trR/QpumqnpvVALjSbLKXDzPdtBGgaaTj634xu7LAYeqmfjef2FesQf3heZEVpVcaSsD+YfPsu6cdYyxdjEJ2DLIjmjnMpIt+HBI7wj777mlHZWnuTGt2jttdY9Quk1aeaYDJjfsuNp9FfQ3u4HvTPK3ftF/Aba6brWL3wvfTcR90s+w4iznxY815erLmcqfXusx15hwrB26nxbTybowDu7WsIYmO0zF8dR24sc7Q9XcwwLUmeljq1nCnOgeY7UXLzrvWfHrSGmFsqMDWuIbwAfupzV6MumtQVtcfB8PA95KoNq1GPpkea9BWbX3CutQCm0t/EUgKGxNa9Tf9tyhD91b/sJ4UZZNRBC1Bs4EsmkOEWN6Sne/tYFDp2puBFkGzc3BxutR7WSSrMEQ5wGn3CDKemOkNYROtkyZm1o2XexNY0GpmiQ0LYmUWE2YsrNah5sNH97Id4/RlooldlzbkO8DugO7sZ7wJ3qrnLVnzGPA9GUBhAxA6FJ+4GI+jPPHyaAzrnKdlnGkLSmpOEi9CxsO8CDu0HBDTuu2K3XTNJBtwg5en8QLL2F8NMPUIdJzrqrJRsF6Od7vd+R6EoOPpuJdxcFDp/AZMK8rK82aoYWqOWvjblhmg1rFNc9w0fcRL3ADzZTrzeu34XjuqZ45eEYQr/wS002aJHoOZrSh63OQUrWW/5M76ykVHcKQ4HaTxftJ/sKJY5TzeoLq3n+pVZfWOCkqYuKPNPo8PTIxYKRD2HMKjAeMhxlQxzgkmglMXqERAQykoxkIyRiRlD5HlG3DLNYJ6TpSzHhydG1xF+7kyXr6gIjpSlQfHyQfI8hZu1MQ53MS5TZgP0PGaWtIxJMdxWu/n4nVeQ6YBEGwoxhISwcOot93iEitnhyjo7CgFCWYBN4++exwsH+IApvh+hChIyJFSAnPGpLJ+/uju/7aEtGhY5FG2RQhnLe7rcPcPEEH/RYmgg9dO+00SnloFeynp7aIkOYCS5GVTsuVceGpOtjBxue+U0AewoV8UG+unxCJBekL0r/TQtG+XwtkG+IP94FfNbAvkPv/ceRN+HiCFpSQUqZBLJhR3bJCAgzIQC1EoKJWPpQyLb2ZytcUZDfnd5iX/WuuJqa68zd+VUV6Zypwbs1Q8OCbsNWIbbHA9PEBowxcltM42ipejIAqAZSBZcQqJgMJPLsNd6dlwFznn7lp737zs/OiawdG52R784cAPQiYYVwohOGfa2wcWPIBvRmJYKhYKZekgPFCEMRTCaKREW/M7LBu7SKs6yuMd3n++pUoQ9c0byeX5fqDz6ViXS/WC29fMfGDatDVwLbnk9/d0vFEfmk1KcD9zEWyWfadnNazpQU/X//KXaVF/+1Nxo0vjtP9x372/el99D2D8ePmvrxefYef2mxvyq/fTN17X/Ld45XY/3snG5mtY1V8z4ZOKPK3eRO/0P1YjI9hTR2VtKwYOoMs0se7z4+U3nkFgf/1tneLROrUQL+4MbndXNDcYv8e2F8Xe4+sC+zSTRfW6YoxUrGY6X42+dtfGy83w9GU0KapvDwpRzSufb5hi0oUpRgIqBUeYc0oIx/LxotSW87nFZcdBkB5wSqePckof5sgPz4YpDgjkWxIJLAFt3sCNeUCZlBR4oUIS9alLKKnTAt5SQrk4RAcXz1tC2ef/AfhySCg4NQ0RVYCxO6YDAW7OJKcUERIic3wfXyaxf1Zcg/TCQdpzkG5eQ/77235E7d++FojB6LV4zcwfXSH3g50xGkKed9cdZJ/PY3Ro+F6q+mJXecJ7q773cuqojG8xl21jlhUf/qYHmZ5ZnNduFQ+trt+RGq0F+Gevrh9WPr938RzDuphIRUMMDgTngFjoghAmFVeESMZBMA/RxQ9FNoc7266buVUG5GQRbeLLCjHvU5g2vm5O6sge2TC+bz/AG7H9wLp+cvc9wpnRsrSY+elu9vY+AOBzfHRahPYndOt1iujnT7Sf/xcr7uSm/+K46bBASkhUCFccC4VD0ZT1mMQqhK4wJIIogi1VHAUEIRFSrhiVYYjEy+UqfnFcmVCuQDYhR5IpSCSRdLWgjgoQxUogJhnCTDR/C+pgGhAsGJMESQUp0KNVyD8BXcmLowuUxYUAniApxWGbkRplgcwQHMYQ85QiLgh2zG8RRBjCFQGa+WeurHtnxec7s+I/DsqK/1jPiuGeJUIWCqmEYiFnrWs/V1r8OeS923Bvcq6LNufawP3Pg3D/cwvuEstQELiLIIThHH8I7tt+3sWfGnf1hLif7cT994Nw/33bLRDufgrOZKbCUB15C2x/2trEOfN4PuCPcPiT5V9x2h87N7/2fvU/UEsHCEhVilJbCAAAHy4AAFBLAQIUABQACAAIAJKz9TxIVYpSWwgAAB8uAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAlQgAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | |||
| + | == Der Satz über die gegenüberliegenden Winkel im Sehnenviereck == | ||
| + | <ggb_applet width="784" height="1092" version="3.2" ggbBase64="UEsDBBQACAAIANuA9jwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7V3bctvGGb5ungLDZnKTEYw9AkikZCTZVmxJdSd23U7HMx2QXFGwIIAGQFtU24tOzu/RB2jOJyeZae7dV+q/WJDCkSR4kCk5mrFIgiscvu8/77/rzXfPTj3tqQgjN/C3Wkg3WprwO0HX9XtbrUF8tGG13n3ntc2eCHqiHTraURCeOvFWi+i4JY8P3Hde+91mdBw80xwvGfLQFc+2WkeOF4mWFvVD4XSjYyHi3HFncOZ6rhMO77Ufi04cXXyhTnLH7w/gKnE4gGOd0+6BG40+3kgu2Pfc+Kb71O2KUPOCzlaLM7h1ePdQhLHbcbytFjXUEbzVwoUv4RCR3x4HoXse+LEcfnHyIziiaZF7LgARSx7bvJE86KYYdDy36zq+fJjkPmCQpj1zu/HxVsu0KJxSuL1juFdk2IY6XScIwu79YRSLU+3sryIM5Fm5DmOH6hNBXOIewY0JedvywzD7KTmNeHpfxDHwEmnOmbhArBe63RFS8v2daCfwuuOv+4Hrx7tOPx6ECackPXQ/Hsrzw6VCecPbfs8T6TEMkB+Lzkk7OLuvQCDq1A+G/eRPkvtp93YDLwi1UMLLYED62lavyRh5o+NRRjLGSEak55AnHX+PbJyMSF7b6jUZ5bm+urX0wdHooZExuowbafKARBFEcfzwntMWQG1LG/hufDD6ACJwkj4qUn/wh8FpG3QgKwTjc6JlnXPzRkF8Nk9E6AtPyYgP1A6CQaQ9lcKorpXcSFd03FP4qL5IIXEkXX+CG1BHu6IXitGNKw1SgCXf5uSwcHjzxugm5D1EcK+dGEwBPE8sn0VqagxaIt91nVgeSUaenjp+V/OdUzhyx4/hOUGLW/IqrtRczTG2WmfbACGcAG21hsnb5C6CQTwacKhuID2bVC9PnArQvTiRs0RMx3gftsaGJkhsRpGQC+rgQbpu8hRy+L10tJdev/14LHGcJgInX9rqxfH6xw5AM1I6zxmCgcmimFzt3tFRJGLtbKu1AWwPQatw5tvDoFuBfCSHK92GP0venCuLm4xRSinNSfKXJJUYhUgJ8z8m2FThXQR552+oCcxy+BSgM7KZBRNhZQSS19QIzIpnCTHHB5lXFMaiL08gtaovRDd1UnFqirQ+nDIxbJnbusCbpngvCPeuG3Y8UcD7UMl2CnAO9JPJkIOAup0xnietvJGLj8GW+CKKEkscZ23uAuLvlhnLG+Tmsk+4kmXKJ1E504OB0xT+U7jRIIw07cxIWR4aI+pGR87QSHmGKD10jjK8gtSE7pm2PRq/PRq1jaWyJo52m6Rn3aajk22zzIOLJ7664UgZdJC7jnsEjDVWyZOSZGw3UcbtsioqP1/ifFmKmDVsdsKuCoBWracbWOeGgWwDmchG1DZNqmSL6AaxmUkRs7FtmcxmyzabZY52GhnMl8iRsm34Uiwp0U2IaLlJiI1s2+am4gfpQBY3KIPgFyGLGHz1/Ow24Wf30vlZGQVYxzaxqE1AOxghiBAVe+jY5Db8s7BhcsTx6hm42YSBmy/TimGU+qhLsmLAC0OmaTAMpoywlCDDZoQzacbAvhnWYgR5w17gFyjaTmMReMFS5jWHpCzleIO8w4PEDqnRjhrdUaO78AL+UEyjVl1+RN74jPPFMDlBqAssGUkkgaFSpIKaKGIW0/xDRaInP41vxHk5T9PQrGTkDumMIpvbzDIsC2yBct1cJ4aNmckQ/FCbpq6T6YhbBoynjBHMaCnLnhSnFUIj97TvuR03HkuaJ9VjnBGCSpUT2hMh+rKScM9/EDp+JCtKakwmUZ6RqM5VI4rqie3GGFymZdo2GXtRxDAybY5MyjkjfEQVs2yOKdh2YhqI8atLVfeKUQXGxQLAMTJMm9kGI2nAQ3ULm4SbhoXBogOLI6aogSnj3ObgopnFri5T4ooxxXVEICiyITQFLbK4Na6wcM5NDPpkIoIpJnRElQnDGTVsgrhBGFlnqvLO/35KVWUhYrvk7tuTfXmR+PZSChG5yGjGQtx8lYgJMlGVNg5r0szztAhwPaRgpyQFR82k4Oj6SEFVcjqsTGXPs9e56iKwWxKBXjMR6F0fEdioyI6H1an0tZKBcu533EwGjq+VDJQS8GF1tr7+MiDO+iHcicQxxfiBOIshnIIvtlpvPBkE8ds3AaD7Tnyu/fq8DW+7rtB6oif85KPnyrdd4Wt/dv0T4WnuqXZfHPvCf+qKEHJ5dY7kunkRieFCrfxV5woCl0RwFDthnNSrtDS3IpBRZX4Slk0dG9kflC2+TAcW54CVoL6lvfF7ZLx9x9cei64oYKdFLuhnHeB3fBj5TKEeDfp9de1f/x3qs2OO1wxzmpYamNUMWJID9mEQOoMoEvH5wO+9NTsa5KWikTSKRCJ0jy4aXpKGiQ0Qm2jUYFEFHNMNWpZVkGDeDEWaQ/F17VHwVAqcL/6+vbN785/a65obxZpw/XlVnM4O8IrnHUvou9GB80D8JW8q86SoWy1xgis5sXTbZhlLQVJObCtrP3AtQTkg20HgCeeiTuomOMKtDkTJ/l+S+GYnbtXMEcITZm6nCx/LCd+OOHYG/biZ/rIrq7+IZhXYShMLQNbIi1C1sOQjuaT5qhDH7YyS+qRGXw7nXnw+OZ5LOoTGOMLogvwhnWADQ3LMTJNYEAZZU4O5aS0Gj+uIQkaZKtaMqpmCMSfsXMyjWKODnhc8e18ceeIswXnW8LqKlOI0S4mULxqR8kWRFKpDugppCbUtYhKM6eVy0mg6ZfmcjJV9Lk3ZrdWULxuR8mWZFMqRhTFDiGALUfZKKcqcpGyP0tA6TfmqESlflc0XRzZm3KLUtAgl6DdNqXbSvBAh/kPTHiWPAe/e1ODXo54DFMCbLQ1Zxn//o72e5Ddy5KO2iC/GdYUX58fN7Ob5olFkLTmXHUXSKUGkrTNeDgyojgnNh/vzBJGP1zKI5BN6K6bLp5mvXEDm/IbTD6K31e9brt8TbYgpswcbxJfm1Y0vkV0SI6RbuaQx3ww3HWsrh/WhG8fC6w/8k1gbgDF/3+m6wtdA50OncxwLf3aYrUX1e3VlwBnSwWoKbN1A2XSQjigws0cNOp8qe+ulyqpLCuMJbezN/P9hLn0pT0q9+LqR//+6CBfTObNNwjAiCNvYIA2gqxbB0zKuxXUtctY6BRfNLIdN2mtyIYC5irjsMJfBlKeMX3zTiJdvirwYOgdXBxpiU4MZkFhWBWYvk5hsh7OSelbd4bwi3uZLPA+nJZ7fNqLt27I6EYticCi2bJTghlmV5CxMm6Tpovkj29F5xdVpt9bMfdeIl+/K6mTZlmUxE1GTgcGzV6JO152XiprA9414+b5CX0BJDEs28lkUVRZqlmblUl7mM3IqbCFXiLT6msEPjUj7oaxMNsbUBNqQYTPK8Up9U3PWrgYvFTHDj414+bGsTMziEC4wCkky4shcBS3IwLmQIfl8xYm5mQuyD8vEPG9EzPPfiFmg0GaXChnj4oXmueJIhDLNjrSTwO8BZn4stB0nciPVDzB7rm1fw1xbljtYulC3UOKobyuYmF+fLppfrxi7Cw/N08l/zBeajEVGTv7OB9p5sqi2QbEMTjEZnmkl9ArtXk3fCcgLKTT1qJbvXGlmUrPPhPVqt2bfaaDuSddiuSDCo80GaNPV75PguX258GRCWdW9iy9lQbI1N3Z5t/1+EDtx0W/fUn77xdfKcd8uOe5bqtDdbOuGiz+ai6C5N8OY1ICNdAi4IXW1OSEUI2u83olzyimSjQcEYU7MRTCuCo1SiG8rhHN45kOknxqFSD9NrXctngn6S613XbAzmrNsHCLJCdCFKlrVSjDmRCnDt1OUQf2eQyHSP1wbpbB0ZBOTy6VlxETpmgS5AsWgPCnAUdtijOPl60Qe8bxuXMCb14+fG+nHz9MKWJa9Cv1YRgFrVeoxQ243ST9SXpSOfD+TjizgPAonWBudobpNwM5CbsAQNaiFx+tmCbZtSi25ppaxhVbWT1CZLAlValPvXn5ppD6/TC1Z8VW6l0VKVuvpXQr0KC36sU6L9ppozN76aAfRCzkzHseu+XbUhTZnmaofle5lr4Ty//7VRCdgdDnksrlp2iYn3DJtPtomcLk6sZyy1GVqRU1dIL80aE94be1NbcdzBvACqgO/98Jfn/ujtq4G5YJpy3+mlQsqUF9VuYCiQvuVVA+mz1UtKJaa/NWUmpZWTLnIoKmlNjEgyF6o1JRfFPXMjaJmdaZpa5jWSHDSrVQ2uE7zfT/1rVcTfMZ761xaarAP1SrqSneuFzZowS0nHyabIRbc7XvKtd4p+dTBZJeqdlYcIzlY8o6TK129O94ylaeANlugm9n1Np2C6ICKi8h1/JLKJ0btvcm8JEt0vdqa3qAuNZsjGVufABMtTaxr4csHj2UY7zYB8O4aQVdTAjWLJdAVoppNX2sFdClVtnUT3OpaGy/W2laB/e06vG83x/j2bLjWtAdPqB4vBO3lmISq3LIM6n4TOPfXR0BrClvmMgtbdQDv1YG511xC99ZN8+tqIlJacz90EWgPIAQpopq1thnnn0O4PxlbGdmMMetfpWhtg+iMYRMRbloWZEkGurWRtnZYBeDVSnqrwMeytjis5+zQDcNSZH1X8dUvxx3NdeHuuulCKQZJN9eGsI5A9MEsjiAWsUxiL6ILlbhWRQc1SB80wfhgfdAtxhijOW5pgRgxqGEyUANKF7LhleDu10G531xo99dNaIuekY1llnETLAsc5aZJ6aqmSdMq9vgDTnOQfC37g8kYF2rZH0xtH1h83UXQKAB8+aXsOXtf71bwU5PJ5Bn7sBFjH06d0K7aN2Nhxq74hPaMU0UVFO6XCfuoEWEfXcIU6gQVW8cp1DkJ26+gZ69Oqz5uRNLHlzCnV0HS1ZvTm8EO1qpSXe7xv08acfXJVJ+1+LKAV8RnHVTFFHUsfdqIpU+n+Slz8carV8NP7dcq1EGZpM8akfTZVN/0m2uaiaO9+vihro/x82n9cMUN09L2t0lO6tXzUTPwVb0t8UxVsSeTGSpuUfxkyf9RwcwcXd+q2WVuWZzfARZraWsSHjUn4bQ9CY8blAhv1qA0bXfYaX0mq6O+okGJjctG2JyxuaTYiRSsphNpae022U4kVY6HyKQepuyD38j+77Ty8+h/pH7n/1BLBwiiOmLODQ8AAMN6AABQSwECFAAUAAgACADbgPY8ojpizg0PAADDegAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAEcPAAAAAA==" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
Aktuelle Version vom 18. Juli 2012, 11:31 Uhr
Inhaltsverzeichnis |
Begriff des Sehnenvierecks
Definition XV.1: (Kreissehne)
- Es sei
 ein Kreis. Die Strecke
ein Kreis. Die Strecke  ist eine Sehen des Kreises
ist eine Sehen des Kreises 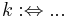 .
.
- Es sei
wenn die Endpunkte der Strecke  auf dem Kreis liegen.
--Nicola 19:22, 25. Jul. 2010 (UTC)
auf dem Kreis liegen.
--Nicola 19:22, 25. Jul. 2010 (UTC)
Definition XV.2: (die Durchmesser eines Kreises)
- Ist eine Sehne, die durch den Mittelpunkt zur Teilmenge hat.
--Nicola 19:22, 25. Jul. 2010 (UTC)
Vorschlag--TimoRR 15:56, 26. Jul. 2010 (UTC): Der Durchmesser eines Kreises ist eine Sehne von k, die durch den Mittelpunkt von k geht.
Definition XV.3: (Radien eines Kreises)
- Das können Sie selbst. Hinweis: Jeder Kreis hat unendlich viele Radien.
- Der Radius ist die Strecke
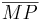 , wenn M Mittelpunkt des Kreises k ist und P ein beliebiger Punkt von k. --Nicola 19:22, 25. Jul. 2010 (UTC)
, wenn M Mittelpunkt des Kreises k ist und P ein beliebiger Punkt von k. --Nicola 19:22, 25. Jul. 2010 (UTC)
Definition XV.4: (Sehnenviereck)
- Ein Viereck, dessen Eckpunkte auf demselben Kreis k liegen.
- Ein Viereck, dessen Seiten Sehnen desselben Kreises k sind.
--Nicola 19:22, 25. Jul. 2010 (UTC)
Der Satz über die gegenüberliegenden Winkel im Sehnenviereck
Die Satzfindung
sehr speziell: Quadrate
Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.
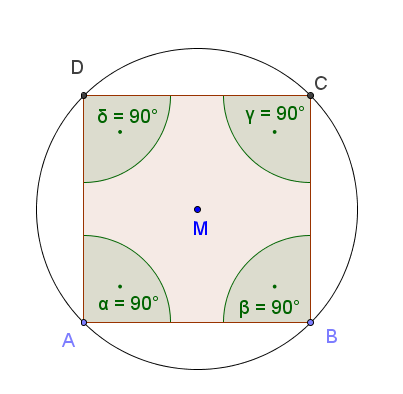
weniger speziell, aber immer noch ziemlich speziell: Rechtecke
Jedes Rechteck ist ein Sehnenviereck.
noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze
Jedes gleichschenklige Trapez ist ein Sehnenviereck.
allgemeines Sehnenviereck
Ausgangslage: 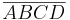 ist ein gleichschenkliges Trapez.
ist ein gleichschenkliges Trapez.
Arbeitsauftrag: Bewegen Sie den Punkt  auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von
auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von 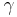 ? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?
? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?
Der Satz über die gegenüberliegenden Winkel im Sehnenviereck

