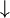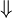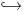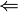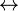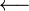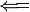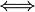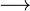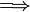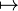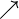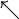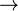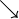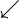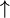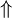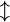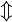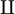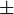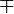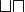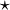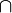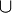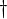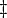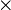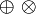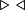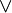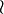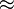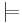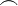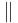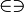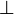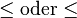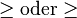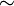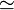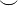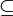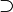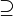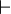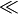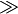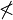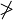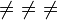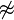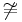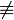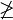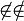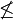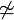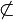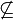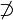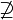Die Geometrie ist eine neue Welt, die man sich mit Hilfe von Axiomen schafft, um darin spielen zu können...
Hat nicht Gott die Weisheit dieser Welt zur Torheit gemacht?
Zur Hilfestellung und Benutzung von Geowiki
Winkel
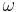


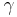
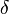
Pfeile
| \downarrow
|
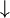
|
| \Downarrow
|
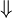
|
| \hookleftarrow
|

|
| \hookrightarrow
|
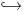
|
| \leftarrow
|

|
| \Leftarrow
|
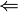
|
| \leftrightarrow
|
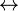
|
| \Leftrightarrow
|

|
| \longleftarrow
|
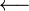
|
|
| \Longleftarrow
|
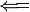
|
| \Longleftrightarrow
|
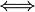
|
| \longmapsto
|

|
| \longrightarrow
|
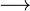
|
| \Longrightarrow
|
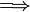
|
| \mapsto
|
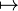
|
| \nearrow
|
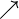
|
| \nwarrow
|
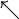
|
|
| \rightarrow
|
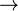
|
| \Rightarrow
|

|
| \searrow
|
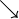
|
| \swarrow
|
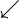
|
| \uparrow
|
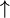
|
| \Uparrow
|
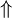
|
| \updownarrow
|
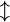
|
| \Updownarrow
|
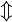
|
|
Binäre Operatoren und Vergleiche
Binäre Operatoren
| Syntax
|
Gerendert
|
| \mathcal{q} (\amalg)
|
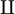
|
| \setminus
|
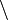
|
| \pm
|
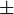
|
| \mp
|
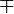
|
\mathcal{t} \mathcal{u}
(\sqcap und \sqcup)
|
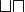
|
| \star
|
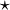
|
| \bullet
|

|
| \cap
|
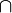
|
| \cdot
|

|
| \circ
|

|
| \cup
|
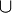
|
| \dagger
|
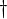
|
| \mathcal{z} (\ddagger)
|
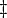
|
| \times
|
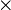
|
| \triangle
|

|
| \oplus \otimes
|
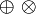
|
| \triangleright \triangleleft
|
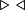
|
| \vee oder \lor
|
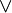
|
| \wedge oder \land
|

|
| \wr
|
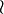
|
|
Binäre Operatoren
| Syntax
|
Gerendert
|
| \approx
|
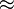
|
| \mid
|
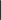
|
| \cong
|

|
| \models
|
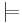
|
| \equiv
|

|
| \frown
|
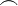
|
| \|
|
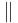
|
| \in \ni
|
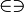
|
| \perp
|
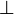
|
| \le oder \leq
|
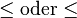
|
| \ge oder \geq
|
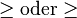
|
| \sim
|
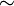
|
| \simeq
|
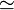
|
| \smile
|
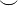
|
\mathcal{vw}
(\sqsubseteq und \sqsupseteq)
|

|
| \subset
|

|
| \subseteq
|
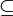
|
| \supset
|
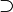
|
| \supseteq
|
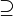
|
| \vdash
|
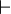
|
|
Binäre Operatoren
| Syntax
|
Gerendert
|
| \ll
|
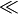
|
| \gg
|
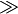
|
| \not<
|
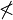
|
| \not>
|
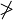
|
| \not= \neq \ne
|
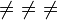
|
| \not\approx
|
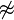
|
| \not\cong
|
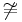
|
| \not\equiv
|
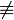
|
| \not\ge
|
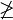
|
| \not\in \notin
|
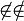
|
| \not\le
|
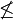
|
| \not\simeq
|
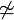
|
| \not\subset
|
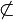
|
| \not\subseteq
|
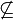
|
| \not\supset
|
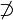
|
| \not\supseteq
|
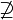
|
| \neg
|

|
|
Hoch- und Tiefstellungen
| Darzustellen
|
Syntax
|
So sieht's gerendert aus
|
| hochgestellt
|
a^2
|
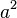
|
| tiefgestellt
|
a_2
|
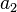
|
| Gruppierung
|
a^{2+2}
|
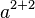
|
| a_{i, j}
|
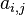
|
| Kombination hoch & tief
|
sowohl x_2^3 als auch x^3_2 ergibt
|
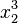
|
| Folge von hoch & tief
|
{x_2}^3, {x^3}_2
|
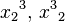
|
| Ableitung (richtig)
|
x'
|
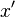
|
| Ableitung (auch richtig)
|
x^\prime
|
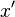
|
| Ableitung (falsch)
|
x\prime
|
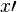
|
| Summe
|
\sum_{k=1}^N k^2
|
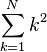
|
| mehrzeilige Summationsgrenzen
|
\sum_{k\in M,\atop k>5} k
|
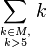
|
| Produkt
|
\prod_{i=1}^N x_i
|
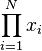
|
| Vereinigung
|
\bigcup_{\lambda\in\Lambda} A_\lambda
|
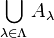
|
| Durchschnitt
|
\bigcap_{\lambda\in\Lambda} A_\lambda
|
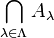
|
| Limes
|
\lim_{n \to \infty}x_n
|
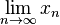
|
| Exponentialfunktion
|
e^{- \alpha \cdot x^2}
|
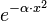
|
| Integral
|
\int_{-N}^{N} e^x\, \mathrm{d}x
|
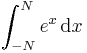 (platzsparend) (platzsparend)
|
| Integral
|
\int\limits_{-N}^{N} e^x\, \mathrm{d}x
|
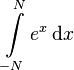
|
| Mehrfachintegral
|
\iint_a^b \iiint_a^b
|
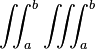
|
| Ringintegral
|
\oint_c
|
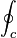
|
| A adjungiert
|
A^\dagger
|
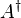
|
Logische Quantoren
Hinweis: Die Verwendung von Quantoren schränkt die Verständlichkeit für Laien und die Lesbarkeit stark ein. Quantoren werden außerhalb der Grundlagen der Mathematik im Regelfall nur als Kurzschreibweise beispielsweise an der Tafel, nicht jedoch in Lehrbüchern oder Fachartikeln verwendet.
| Darzustellen
|
Syntax
|
So sieht's gerendert aus
|
| für alle x
|
\forall x \, A(x)
|
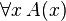
|
| es gibt ein x
|
\exists x \, A(x)
|
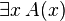
|
| alternativ:
|
| für alle x
|
\bigwedge_{x} A(x)
|
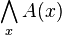
|
| es gibt ein x
|
\bigvee_{x} A(x)
|
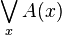
|
Vorlage:Vorlagenname
Tabellenvorgaben
bla
|
|
Beweisschritt
|
Begründung
|
| (I)
|
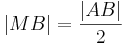
|
bla
|
| (II)
|

|
bla
|
| (III)
|
 ist der Mittelpunkt von ist der Mittelpunkt von 
|
bla
|
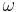


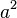
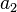
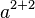
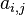
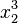
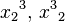
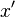
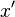
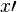
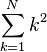
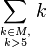
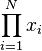
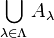
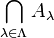
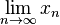
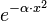
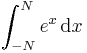 (platzsparend)
(platzsparend)
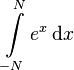
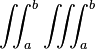
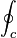
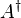
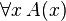
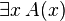
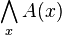
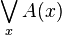
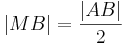

 ist der Mittelpunkt von
ist der Mittelpunkt von