Lösung von Aufg. 11.2 S: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Lösungsversuch Nummero6/Tchu Tcha Tcha:<br /> Skizze folgt..<br /> Voraussetzung: Dreieck (<math>\overline{ABC}</math> )<br /> Annahme: mindestens 2 Innenwinkel …“) |
|||
| (10 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | == Aufgabe 11.2 == | ||
| + | Beweisen Sie:<br /> | ||
| + | <u>Korollar 1 zum schwachen Außenwinkelsatz</u><br /> | ||
| + | ::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.<br /> | ||
| + | |||
| + | |||
Lösungsversuch Nummero6/Tchu Tcha Tcha:<br /> | Lösungsversuch Nummero6/Tchu Tcha Tcha:<br /> | ||
| − | + | [[Datei:Übung 11.2.png]]<br /> | |
Voraussetzung: Dreieck (<math>\overline{ABC}</math> )<br /> | Voraussetzung: Dreieck (<math>\overline{ABC}</math> )<br /> | ||
| − | + | Behauptung: mindestens 2 Innenwinkel sind spitze Winkel (Größe: kleiner 90)<br /> | |
| − | + | Annahme: genau 1 Innenwinkel ist ein spitzer Winkel<br /> | |
oBdA.: <math>\left| \angle ABC \right| = \left| \angle BAC \right| = 90</math> | oBdA.: <math>\left| \angle ABC \right| = \left| \angle BAC \right| = 90</math> | ||
Nach dem "Schwachen Außenwinkelsatz" gilt: | Nach dem "Schwachen Außenwinkelsatz" gilt: | ||
| − | <math>\left| \beta' \right| | + | <math>\left| \beta' \right| > \left| \angle BAC \right| und \left| \beta' \right| > \left| \angle ACB \right|</math>. |
<br /> | <br /> | ||
Da <math>\beta'</math> der NW von <math>\angle ABC</math> ist und nach dem Supplementaxiom und Def supplementär gilt:<br /> | Da <math>\beta'</math> der NW von <math>\angle ABC</math> ist und nach dem Supplementaxiom und Def supplementär gilt:<br /> | ||
NW_1+NW_2= 180 ,und daraus nach Rechnen in R folgt, dass <math>\left| \beta' \right|</math>= <math>\left| \angle ABC \right|</math> = 90 ist,<br /> | NW_1+NW_2= 180 ,und daraus nach Rechnen in R folgt, dass <math>\left| \beta' \right|</math>= <math>\left| \angle ABC \right|</math> = 90 ist,<br /> | ||
| − | kann <math>\left| \beta' \right|</math> nicht größer als <math>\left| \angle | + | kann <math>\left| \beta' \right|</math> nicht größer als <math>\left| \angle BAC \right|</math> sein (,da <math>\left| \angle ABC \right| = \left| \angle BAC \right| = 90</math>) ..<br />Widerspruch zur Annahme. Behauptung stimmt. qed<br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:04, 5. Jul. 2012 (CEST)<br /> |
| + | *Also die Behauptung stimmt so nicht. Ich glaube, dass hier Annahme und Behauptung vertauscht/verwechselt wurde. Der Beweis sollte noch einmal überarbeitet werden, da du eigentlich zu keinem Widerspruch zur Annahme, sondern zu einem Widerspruch zum schwachen Außenwinkelsatz kommst.--[[Benutzer:Andreas|Tutor Andreas]] 11:11, 10. Jul. 2012 (CEST)<br />Ja stimmt, Behauptung und Annahme wurden vertauscht. Habe es jetzt geändert. Müsste doch jetzt passen, wenn ich annehme, dass 2 Innenwinkel rechte Winkel sind und dies zum Widerspruch führe, oder? --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:15, 10. Jul. 2012 (CEST)<br /> | ||
| + | *Ich würde sagen, dass es fast passt. Was wäre denn, wenn die Winkel aus deiner Annahme größer 90 sind? Deine Annahme ist noch ein bisschen zu speziell. Besser wäre, wenn man annimmt, dass zwei Winkel <math>\ge</math> 90 sind. --[[Benutzer:Andreas|Tutor Andreas]] 11:42, 16. Jul. 2012 (CEST)<br /> | ||
| + | Auch dann gibt es einen Widerspruch zum schwachen Außenwinkelsatz. Angenommen der Winkel ABC ist größer 90, dann müsste der NW (beta') kleiner 90 sein. Da es noch einen zweiten Innenwinkel in diesem Dreieck größer 90 geben soll, wäre dies zum schwachen Außenwinkelsatz (beta') ein Widerspruch..--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 15:48, 18. Jul. 2012 (CEST)<br /> | ||
| + | [[Kategorie:Einführung_S]]<br/> | ||
| + | <br/> | ||
| + | Weitere Lösung:<br/> | ||
| + | <document>RitterSport_IMG_0001.pdf</document><br/> | ||
| + | --[[Benutzer:RitterSport|RitterSport]] 13:13, 10. Jul. 2012 (CEST) | ||
Aktuelle Version vom 18. Juli 2012, 14:48 Uhr
Aufgabe 11.2
Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Lösungsversuch Nummero6/Tchu Tcha Tcha:
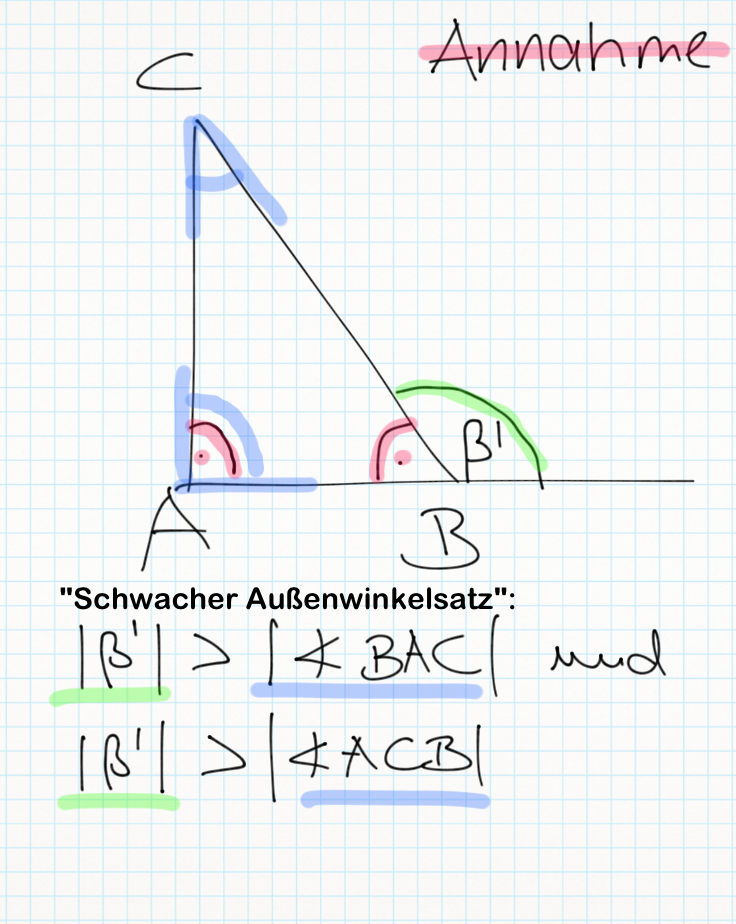
Voraussetzung: Dreieck (
)
Behauptung: mindestens 2 Innenwinkel sind spitze Winkel (Größe: kleiner 90)
Annahme: genau 1 Innenwinkel ist ein spitzer Winkel
oBdA.: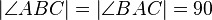 
Nach dem "Schwachen Außenwinkelsatz" gilt:
.
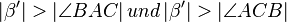Da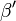 
der NW von 
ist und nach dem Supplementaxiom und Def supplementär gilt:
NW_1+NW_2= 180 ,und daraus nach Rechnen in R folgt, dass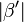 
= 
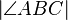= 90 ist,
kann 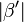nicht größer als 
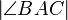sein (,da ) ..
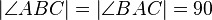Widerspruch zur Annahme. Behauptung stimmt. qed
--Tchu Tcha Tcha 13:04, 5. Jul. 2012 (CEST)
- Also die Behauptung stimmt so nicht. Ich glaube, dass hier Annahme und Behauptung vertauscht/verwechselt wurde. Der Beweis sollte noch einmal überarbeitet werden, da du eigentlich zu keinem Widerspruch zur Annahme, sondern zu einem Widerspruch zum schwachen Außenwinkelsatz kommst.--Tutor Andreas 11:11, 10. Jul. 2012 (CEST)
Ja stimmt, Behauptung und Annahme wurden vertauscht. Habe es jetzt geändert. Müsste doch jetzt passen, wenn ich annehme, dass 2 Innenwinkel rechte Winkel sind und dies zum Widerspruch führe, oder? --Tchu Tcha Tcha 13:15, 10. Jul. 2012 (CEST)
- Ich würde sagen, dass es fast passt. Was wäre denn, wenn die Winkel aus deiner Annahme größer 90 sind? Deine Annahme ist noch ein bisschen zu speziell. Besser wäre, wenn man annimmt, dass zwei Winkel
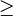90 sind. --Tutor Andreas 11:42, 16. Jul. 2012 (CEST)
Auch dann gibt es einen Widerspruch zum schwachen Außenwinkelsatz. Angenommen der Winkel ABC ist größer 90, dann müsste der NW (beta') kleiner 90 sein. Da es noch einen zweiten Innenwinkel in diesem Dreieck größer 90 geben soll, wäre dies zum schwachen Außenwinkelsatz (beta') ein Widerspruch..--Tchu Tcha Tcha 15:48, 18. Jul. 2012 (CEST)
Weitere Lösung:
<document>RitterSport_IMG_0001.pdf</document>
--RitterSport 13:13, 10. Jul. 2012 (CEST)
