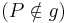|
|
| (10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) |
| Zeile 60: |
Zeile 60: |
| | |} | | |} |
| | | | |
| − | Bemerkung zum Nachweis der Korrektheit, desjeweiligen Schrittes: Gemeint ist eine Begründung, aus der hervorgeht, dass der jeweilige Schritt (ggf. eindeutig) ausführbar ist.--[[Benutzer:*m.g.*|*m.g.*]] 13:10, 27. Okt. 2011 (CEST) | + | Bemerkung zum Nachweis der Korrektheit des jeweiligen Schrittes: Gemeint ist eine Begründung, aus der hervorgeht, dass der jeweilige Schritt (ggf. eindeutig) ausführbar ist. |
| | | | |
| | ==Definition des Begriffs== | | ==Definition des Begriffs== |
| | =====Definition 2.1: (Spiegelung an der Geraden <math>\ g</math>)===== | | =====Definition 2.1: (Spiegelung an der Geraden <math>\ g</math>)===== |
| − | ::Es sei <math>\ g</math> eine Gerade. Unter der Spiegelung <math>\ S_g</math> an der Geraden <math>g</math>versteht man eine Abbildung der Ebene auf sich, bei der die Gerade g auf sich abgebildet wird und der Punkt P so abgebildet wird, dass gilt: <math>\overline{P\rho(P) } \perp g</math> und <math>|Pg| = |g\rho (P)|</math>. | + | ::Es sei <math>\ g</math> eine Gerade. Unter der Spiegelung <math>\ S_g</math> an der Geraden <math>g</math>versteht man eine Abbildung der Ebene auf sich, ... |
| − | | + | |
| − | Zweite Möglichkeit (etwas einfacher und plausibler ausgedrückt):
| + | |
| − | | + | |
| − | ::Es sei <math>\ g</math> eine Gerade. Unter der Spiegelung <math>\ S_g</math> an der Geraden <math>g</math>versteht man eine Abbildung der Ebene auf sich, bei der die Gerade g auf sich abgebildet wird und Mittelsenkrechte der Strecke <math>\overline{P\rho(P) }</math> ist.
| + | |
| − | <br />
| + | |
| − | --[[Benutzer:HecklF|Flo60]] 20:29, 31. Okt. 2011 (CET)
| + | |
| | | | |
| | ==Die Geradenspiegelung als spezielle Bewegung== | | ==Die Geradenspiegelung als spezielle Bewegung== |
| Zeile 83: |
Zeile 77: |
| | =====Fall 1===== | | =====Fall 1===== |
| | ::<math>\ A, B</math> <math>\in</math> <math>\ g</math> | | ::<math>\ A, B</math> <math>\in</math> <math>\ g</math> |
| − | Beweis: <br /> | + | '''Beweis:''' <br /> |
| − | Nach der Definition 'Bild eines Punktes bei einer Geradenspiegelung' und des Satzes, dass die Zwischenrelation eine Invariante der Bewegung ist, ergibt sich das von selbst. --[[Benutzer:HecklF|Flo60]] 20:53, 31. Okt. 2011 (CET)
| + | |
| | | | |
| | =====Fall 2===== | | =====Fall 2===== |
| − | ::<math>\ A</math> <math>\in</math> <math>\ g</math>, <math>\ B</math> <math>\notin</math> <math>\ g</math> | + | ::<math>\ A</math> <math>\in</math> <math>\ g</math>, <math>\ B</math> <math>\notin</math> <math>\ g</math><br /> |
| − | Beweis:<br />
| + | '''Beweis:''' |
| − | Den Schnittpunkt von <math>\overline {BB'}</math> mit <math>\ g</math> bezeichnen wir mit <math>\ L</math><br />
| + | |
| − | Zunächst eine Skizze zum 'spielen': Bewege Punkt B nach belieben.
| + | |
| − | <ggb_applet width="1366" height="607" version="4.0" ggbBase64="UEsDBBQACAAIAEWpXz8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAEWpXz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vhtb9s2EP7c/QpCH/aplknxRVbndGgGDCuQrgPSDcO+DJTEyFxkSRNpJxn243ckJVu217Rp2u4laEpRPN7xnrvnjsry69t1jbaqN7ptziIS4wippmhL3VRn0cZezRbR18+/WFaqrVTeS3TV9mtpzyLmJHV5Fi1UlmSYZDOBCzpjuShnWcL4jNFC5ARLUog0QujW6GdN+71cK9PJQl0WK7WWF20hrTe8srZ7Np/f3NzEo6m47at5VeXxrSkjBMdszFk0PDwDdQebbqgXTzAm859fXQT1M90YK5tCRci5sNHPv3iyvNFN2d6gG13aFThMF0mEVkpXK3AqZSxCcyfVASKdKqzeKgN7J1PvtF13kReTjVt/Ep5QvfMnQqXe6lL1ZxGOKefJIiFZlhLMhbPR9lo1dpAlg835qG251eomqHVP3iJssm1b59JpRH/+iRKcYPTUDSQMCQxChCUc3mEahiQMLAw8yLCwnQVRFmRYkGE0QlttdF6rs+hK1gYg1M1VD+HbzY29q5U/z/Bi7z15Cj4Z/QcIUwx5EjCH9xg/db8CfplbmB86SSZWbb95oNHRJKFCvL/N5FGe0tEoy8ipzYS/xU9xj9Hg+Hs5yifYgin/z/+eWKT3uXlsMcwfZ1Cwz+Licj5yZTnQA5mVkx3Sx6q1cYShGeKZy3uCOJBDpJDmHJEMhjRBQAdEOGIcpmSBhBtTRFNYYIiiBXJyhCLPDr6A/1jqlQnEQZl7mwIpEQFDDHGKiCcVQ0Al5IkJJE0oSHCOOGxy5kniVFCBmIAZXSAGZ3ScTAkIUtgIczCfIEoQdZtJihKBhNNHmOO6WLijg8oECYwEcQqB1kDpQGeQXyDqvBEDXLrpNvYAomJdjo+27XaxAGkoSPuyFwrUQVV8sqxlrmroFJcukghtZe0Y4Q1dtY1FYxCT8K7qZbfShblU1sIug36TW3khrbr9FqTNaNvLFm1jfuhb+01bb9aNQahoa7w7c1uTyXOyOzVM6GSBTRf4ZEFMntO/tdvCCtoYBfbb3ozisixfOol9aQAkXzf13Xmv5HXX6kM3lnPfdJZqU9S61LL5CZLVWXG4oH0PcvVq7EE8zcaTtH15eWcghdHtL6pvoVYRHuPpD5Sfu7BEj5dApSmkYx/HhytArru3LnnTarsLkbxVe2+r3lF7Mnlpztt6/8oD8I3s7Kb39wc4Xu+8etFUtfJJ4ustNOfiOm9vL4dyHXS9uetghsMJ8soDj6A4JJyDwDDmYfQy7mg7KexlsJfAY7rpcrdOssRL+DEPo5eC/A1HG1wlo5sEj2a08SUNRwNxxnLlst+1+k2j7cU4sbq4HlwlYcP3m3Wudjl0qJN8LJ3L+VGSLa9V36h6yGkI5qbdmEDRSbqXqtBrmIaFARLpwvUjHCC8LVXVq/Hgtb+bBcD8Kp5m68lrr+rbvl2/bLZvIBeODrCcj6dcmqLXncs5lEMfuFb7rCq1kdBGyuk+R0JwvXDtAuCxDhqg58au2t7fvqCqwOi4V6s13LWQ9enlM3QH8wt/iXN4ojb/DQrbrveF9X3AYPlvU80npay7lXQXvcHpWt6p/gAGr+9VWx6DA9h7D4DknVPgotspFRIjnBgeOlDo+XRQpwBvg27dTdw197uzaIZjBqz/I1zjwzXWuetodlCbw9ujWEECBaTegdn5r+QUtcPs/U/AlsWZRy2JxccBrWjXa9mUqPFXnAsoK9G+40rssg1JEgAM4GzsuFQFZYOKkwi4GrVDt3p00uL3xv711ZVR1sHlPuJcjjF6X2j28M5oTEJa8pgvAsAixoyflF0LV4Jr+PAxvjfYoQv4h+90WSp/HQxt6fcmbDGhFup1V+tC2wel7/+B8mPuQsp+itx9pfu+7Y+y9zxkb3WSu+dfyq41X92fwUdBGLb8o6HYw7mIORUZFpxBenKRCg8ujVmWLhh8Xy8Y/AiefgKoL1Xl3h9jPeAT6sUJ4vn9WJtB54hj/g6cJyk2BZrg5ODe5eePBzuJGT2AVQypTAXFGWWcs5TRhBGP9iyB8pFmEIkk4bApy8T71A/CH1xAPMK1I93LxsLVSvm7xemN6Vqpzl1VXzdvetkY9/ewIDO5ib0l2DvFR+GuQqDzk0BfPIRUFx9EJ/edXoUhD8PjQ0wEiwVmKSYiyYBRlPsQMxyLLKFZCisJxDNEmKTxgouTT5BPyK4Xb+NV8TBeFR/GK3zyNfMRIJ+RmB+12ywmlN7XbemHd9vPQJb7Y7fvOQcRLB8WwfLfFEEaZ/y43zjWxAk5ak6ONVmMaSqYSDkjgmSY/4cCPZ9+vfm/kgx/8n/+F1BLBwjr8EUlxwYAAI8YAABQSwECFAAUAAgACABFqV8/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAEWpXz/r8EUlxwYAAI8YAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAXgcAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
| + | |
| − | <br />
| + | |
| − | <br />
| + | |
| − | Zu zeigen: |AB| = |AB'|<br />
| + | |
| − | Direkter Beweis<br /><br />
| + | |
| − | Fall I: <math>A \in \overline{BB'}</math>: Nach Definition Mittelsenkrechten und Bild eines Punktes bei einer Geradenspiegelung ist dieser Fall bewiesen.<br /><br />
| + | |
| − | Fall II: <math>A \not\in \overline{BB'}</math><br />
| + | |
| | | | |
| − | Nach der Definition Bild eines Punktes bei einer Geradenspiegelung und Defintion Geradenspiegelung ist g die Mittelsenkrechte von <math>\overline{BB'}</math> <br />
| + | =====Fall 3===== |
| − | Daraus folgt: |BL| = |LB'|<br />
| + | |
| − | A und L liegen auf g, danach gilt nach der Reflexivität von '=', das |AL| = |AL|<br />
| + | |
| − | Da das Mittelsenkrechtenkriterium einen Winkel von 90 vorschreibt, sind auch die beiden Winkel <math>\angle BLA</math> und <math>\angle ALB'</math> kongruent zueinander.<br />
| + | |
| − | Nach SWS, der Definition von Kongruenz und den drei vorherigen Beweisschritten ist klar, dass |AB| = |AB'| ist.<br /><br />
| + | |
| | | | |
| − | Wirtschaftlicher wäre der Beweis mit dem Mittelsenkrechtenkriterium zu führen, dort hätte man nur einen Beweisschritt. --[[Benutzer:HecklF|Flo60]] 21:17, 31. Okt. 2011 (CET)
| |
| − |
| |
| − | =====Fall 3=====
| |
| − | <ggb_applet width="1280" height="857" version="3.2" ggbBase64="UEsDBBQACAAIAFGfZz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vrdbts2FL5en0LQxe6i8F8iZrdwOgwokK7F0hXbbgZaom0tsuRJcuL0rdb2OfpMOyRlW7LjpE7cNSnmC8sij47I7zvf4aHk3rPFNPMudFmlRd73cYB8T+dxkaT5uO/P69FR5D97+qQ31sVYD0vljYpyquq+TwPim/Z5+vTJd71qUlx6KrMmb1N92fdHKqu071WzUqukmmhdd9rVfJFmqSqvXg3/0nFdrTuckxf5bA53qcs5tMXT5DStlqfH9oazLK1/TC/SRJdeVsR9X3AYOvx6q8s6jVXW9xlyLaTvk41OaKKmd1KU6bsir4352nmmhjoDAM7qq0x73oXppa5rBMaeV6XvNIBFTFvv2GLQ0/M4S5NU5Waedohg5HmXaVJPjG1kbqfT8QTmEXHu3MVFUSZnV1Wtp97iD10WMFTMDQlX7oy6swrGDHfkyHa1z6wbfXGm6xpGXHlqoddgjss06Zy8qE6KbN00K9K8fq5m9by0fNOmyU6878O9SjPgQT7OdNNGgI6Jjs+HxeLMoUCd6zdXM3uJHdBw/LzIitIrDfQcDJrj0B2tjRnpygpZG2QtGh/G6aofS2It7HHojo6rNHdDa2aOl7PGaHmbtPJMg4ERwnQ1ecty3/e9eZ7Wp8sTCI/zZqrYXfDzfDoEfbQDZOUTH8pn73gjfnrnusx15oIkB27nxbxyoejuZQeS6DidwqnraCBRhq5fYQCuNdHjUi8H7tTlALO9qB2IG8294+UgzBgqGGtcQ5qA+dRmLj+pLKNGyjXIqO+/1jVo8fV8OtWZ7yWqBhOTInSmpxpUU9sAsfG1Aup3f5U9CpsINpFcYw7910aLjSuVzSYKWpaCyNQVjKU9QevvZZF0p61ygM/OCSQ4Mw4MQTOtkyYX1k1UezNwaTXSQt+CVnmLvn+EAiFAmfCLBJHvvXOXWyunKJMM1okE6Hao3ILPb98IPjwQqPPhFixwsSdYcTGdqjzxcjWF+56C+C1CqVkuPIUMYp7CJrAcKPN62TF2rhoHW7ibPLJCdex3U0s9AQXnuqps/qvbma7DjVuuPpsadHdi1tDSIIpc5ImAdFDGFtojzAIpwq10ecOc9N+5s6lc0kqnsNrGab1P5A62I3dPdB5E4GLAzqFLA7P0HErYJ98GPNEq+EhAuwqn9xH2y7Qsi3JD2gMn7fGWtAffq1lR/XCzwDfCs7nkq7LQWT+YDCkPcRgiyQlDxMIKLhkLEcdUEAY1pKRcHBzXk124nuyP68nDwpUFiBIiBeaMhJjL0KLKA04wkZyGUgoaifA+kJ7psWnfxLTBwSJ7soWsuhnTqvG5xEsdYj1qCbiNOsdb5fkBgA+DqAOxyxIsiBgEOI0YD0nEEHMrFI8geVBoNREOvZgfaLGymGcmf73IoTittK1ft8voc61nZv/yKn9Tqrwye1xn0yrPd9C/crwRAGqXqE7/HO4jKGN+FzEJZmk1h6E7HEBNNAw4JCkaCgYVBcOuiEMyMPqiEUESc1CZZVWEAVDNVusBOZy4Bm1xDbYQvgXfTXENv6C4XEojiB2y3pOiuyRYFkgAmmovIMv1NxIE4QiJEL4YZt+AtMaO+OE10rolr25KSz0YaREeYEI5ocAcsMuisKnpRcAFx4JBUowwEo5VygLKqWhV+l9GW60CoAN0vJ/C4i+usAPup454wELBJSKQ7gjh4XLp4lBHcEopCE9E1NUMUPZKIihBhFJEZAi579HIawf/u0qWZD/Ok0fFOQ4Elu2Pk58Adrd31BRBuYJbW2326Elvi74pUDrk6/3I17vJp/clf/k82dGPzUbpIAEAaVYycE5DhgSjS/6h3kGcmPIGIyqbJyoBiqSQEANhKAR8hTcEwOaEH2QAGM53VFOj/agfPTbqYTNIgfBQRFJGWFK38T5isCEXmEUoDDGUVbKhnkQBE9AjJWUhFRI/Iurta5zr073jn1yX9z/9c3MA2LcNK+bA2lwPI5o3gOOAgKQYNzKB9RMRfp8Hpxhtp338mdTTPdK0KuN1ISWXb6yyrLj8RY8yvbBY3gd4U3x2od+W3qf3e0H/fhN6WKfgwyG6oZqRkN7YfaBvHswgdgfo0V2hN3wfHPut5c7i3+weugx82IuBD/8z8HkMnFzLwGDHduPTx71Y+HhrCiL/bQp6NRpVurZ1hnuZ8PUpOm6/0LV/Ymj+4PH0X1BLBwj3CldhZwYAABIiAABQSwECFAAUAAgACABRn2c/9wpXYWcGAAASIgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAKEGAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| |
| | ::<math>\ A, B</math> <math>\notin</math> <math>\ g</math>, <math>A</math> und <math>B</math> liegen in derselben Halbebene bezüglich <math>g</math><br /> | | ::<math>\ A, B</math> <math>\notin</math> <math>\ g</math>, <math>A</math> und <math>B</math> liegen in derselben Halbebene bezüglich <math>g</math><br /> |
| | | | |
| − | Beweis:<br>
| + | '''Beweis:''' |
| − | | + | |
| − | Sei <math> L_a := AA' \cap g </math> und <math> L_b := BB' \cap g </math><br>
| + | |
| − | nach Definition der Gradespiegelung ist g Mittelsenkrechte von <math> \overline{AA'} \wedge \overline{BB'}</math> <br>
| + | |
| − | <math>\Rightarrow L_a \wedge L_b </math> sind Mittelpunkt der Strecken <math> \overline{AA'} \wedge \overline{BB'}</math><br>
| + | |
| − | <math>\Rightarrow \left| AL_a \right| = \left| A'L_a \right| \wedge \left| BL_b \right| = \left| B'L_b \right|\box </math><br>
| + | |
| − | Ferner gilt da g Mittelsenkrechte ist <math>|\angle L_bL_aA'|=|\angle AL_aL_b|=90\box \box </math><br>
| + | |
| − | Trivialerweise gilt <math>\left| L_aL_b \right| = \left| L_aL_b \right|\box \box \box </math><br>
| + | |
| − | Aus <math>\box ,\box \box ,\box \box \box , SWS \Rightarrow \overline{A'L_aL_b}\equiv \overline{AL_aL_b} \Rightarrow \left| A'L_b \right| = \left| AL_b \right| \wedge \angle A'L_bL_a\equiv \angle L_aL_bA \Rightarrow \angle B'L_bA'\equiv \angle AL_bB</math><br>
| + | |
| − | Nun gilt: <math>\left| A'L_b \right| =\left| AL_b \right| \wedge \left| B'L_b \right| =\left| BL_b \right| \wedge \angle B'L_bA'\equiv \angle AL_bB </math><br>
| + | |
| − | <math>\Rightarrow \overline{A'B'L_B}\equiv \overline{ABL_B} \Rightarrow \left| AB \right| =\left| A'B' \right|</math>
| + | |
| − | --[[Benutzer:Peterpummel|Peterpummel]] 19:42, 7. Nov. 2011 (CET)
| + | |
| | | | |
| | =====Fall 4===== | | =====Fall 4===== |
| | ::<math>\ A, B</math> <math>\notin</math> <math>\ g</math>, <math>A</math> und <math>B</math> liegen in verschiedenen Halbebenen bezüglich <math>g</math><br /> | | ::<math>\ A, B</math> <math>\notin</math> <math>\ g</math>, <math>A</math> und <math>B</math> liegen in verschiedenen Halbebenen bezüglich <math>g</math><br /> |
| − |
| |
| − | Beweis<ggb_applet width="1280" height="857" version="3.2" ggbBase64="UEsDBBQACAAIABu1Zz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VrLcts2FF03X8HhojvTeD+mUjJ+bDLjNJlxmmm76VAkJLGmSJWk/MjX9wIgJUqynChWJlayYQiAIHDOPedeUB68uZ/lwa2p6qwshiGOUBiYIinTrJgMw0UzPlHhm9evBhNTTsyoioNxWc3iZhjSiIS2fZG9fvXLoJ6Wd0GcuyGfMnM3DMdxXpswqOeVidN6akyz1h4v7rM8i6uH96N/TdLUqw4/ydtivoC3NNUC2pJZepXV3e2pe+E8z5rL7DZLTRXkZTIMBYelw/8+marJkjgfhgz5FjIMCcZrndBEbe+0rLLPZdHY4avJ83hkcgDgunnITRDc2l7qu8YwOAjq7LMBsIhtG5w6DAZmkeRZmsWF3adbIgwKgrssbaZ2rLKvM9lkCvtQnPvpkrKs0uuHujGz4P5vU5V2qdyS8ODvqL+rYc3wRo5cV//OTWNur03TwIrrIL43KzAnVZau3bytz8t81TQvs6K5iOfNonJ807bJbXwYwrsqu+CzYpKbtg1wTKYmuRmV99ceBeqn/vgwd4+4BY0mF2VeVkEF+4G9BpP2OvJXN8audDkKuTHIjWjnsJMu+7EmboS7jvzVc5UVfmntznG3a4y612R1YBssjBCmy807lodhGCyKrLnqbiA8blZbtQ/8vpiNQB/9AFnOiQ815+B0I34GN6YqTO6DpABuF+Wi9qHo3+UWkpokm8Gt72ghiS1df8ACfGtqJpXpFu7V5QFzvagfiBvNg9NuEXYNNaw1acAmYD+N3YtVcQMKGoYfTAMy/LCYzUweBmnc2F6ridzMDAimcbHhQmuJ0Z/h0jhK5wGbIK7ghv5HA8WFVJzPpzG0dFrI4wdYS39vbr53Zbq+47gA5Nx2QH1zO4HlZm6Mp7VpwzmYw4ROHD3YHVp1cD8MT3CkFOr/g2cf7GwqDD57Q3WPeF1ZS1jZCZDuAfoCVH/9FFCJSKwBhXiLlBD7QZWUs1lcpEERz+C9V2AADp/MpowgRja0ghhb2Dwki6briP1U7QRbqFsvWWIah+v20kxBxYWpa6uz5Z5Pt5jxKaudpAfELmbQt/OywhYYYQ5NFTEfeCci4gSpflyefvWGzH+FH1N718pmkG6TrNknaM+2g3YNmqOIWQRVjoWVgcoPp+fznwEaFRGPzQmJEHuOgt9lVVVWGxo+8xqOtzR89ms8L+vfnlbyRii2j/xQ1PtBhQTDSmCFEdIUMyE9kDSiTDAqEQWnlISoZxnjo7Ce74L1fH9Yz18WrCqiSBGATxMuBcbKgQqYIo44NCmlBWb6OZBem4ltfzxUe4G5huzoaUzrds4Or9Ex5R1rAmsR6wMZHIVyhanCSmskFKfeIKBDK8Ix1xIoERpheqCs5BDPrV29LaAWrY2rVLcL5htj5vak8r74WMVFbU+zfkyvEN+L/E4ELgTOt8hP9iM/OSbyOdhVT1q84x6pvgwhNjz3jEUYC8o0pxwiQxwR9cuJN8gf7XLTq3++UGquO6kd/i0uKpjj1F5G/vJ8VnVEsKQcYYU0I1x5WjmNgGqqFVWKE4J9NSR0JGV3Et/PSndBGntIk0cg/YKRbkI6ejGQUskioYjL+kQIe94BSImKhJSSaE0wx4T7zMRAVVSxzbL9gHlq26TS/Uwq3W1S/Lkm1X0t8jbF8SHgF5Em7eEIkY2jujMmBEclLL7qpLS5wReZk87WctKOssTsR7o5MtLh/Cs4Zr7mQ5RK1YYAYQy5xMSFUIi4EAApItAglCmUSaLI0UeATSiO/dY115gf78f8+Dsyb7ne+DZ8mK8hFFIXx1CCMEUxkrwlH1OCiFIQAIqyTv8iIpwSQoF4AWWrlsfD/q4smnr2zRb3F/vk0IsXk0E5V5FkVFPOuKaK+wwqeSQgp0JVgqFW0bw9LmMUwUg4Z1BFuZBUHDyFXmzhOtlPU5PdmtIH0pS9HE5SULtrgF4hqx2wSt19FhOYCujBUiAQjxcUYREXhCFQH5JIgOSeUNTmfl+kn65l1G32p/uxP93NvnyR7J+wCFEMtb/mnFEuUUe/1hKaiQSHBWv1foqh3lKYM2iSGiJFPEH+5nZ/MPkfnP2tUz/eYvtyHw+9/CYPheOA/7mTHCAxHuZ7LzgAWC1FUCbZMx/R7a83EiGuMWFQazE4znyHz2t97V1usZHtp73sO1YzB//CYnXHJFQsREqmSfeTGbRKiRmjUK0KrbG3XUwjKHQF8AFlj4ZjzFOu+8PrmNP+L8ruryjavzB5/T9QSwcIuw/fso8GAACTIgAAUEsBAhQAFAAIAAgAG7VnP7sP37KPBgAAkyIAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADJBgAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| |
| − |
| |
| − | Leitgedanke:
| |
| − | Die beiden Dreiecke BB'C und AA'C sind gleichschenklig (trivial)<br>
| |
| − | Es gibt den Schnittpunkt C = AB geschnitten A'B', wegen A und B befinden sich in verschiedenen Halbebenen + wäre wenn nicht widerspruch zur gleischenkligkeit (mittelsenkrechtenkriterium)<br>
| |
| − | und daraus würde dann die Gleichheit folgen.<br>
| |
| − | müsste noch ausformuliert werden.
| |
| − | --[[Benutzer:Peterpummel|Peterpummel]] 22:23, 7. Nov. 2011 (CET)
| |
| | | | |
| | == Eindeutige Bestimmtheit von Geradenspiegelungen == | | == Eindeutige Bestimmtheit von Geradenspiegelungen == |
| Zeile 141: |
Zeile 97: |
| | ==== Satz 2.2 ==== | | ==== Satz 2.2 ==== |
| | :: Jede Geradenspiegelung ist durch die Angabe ihrer Spiegelachse eindeutig bestimmt.<br /><br /> | | :: Jede Geradenspiegelung ist durch die Angabe ihrer Spiegelachse eindeutig bestimmt.<br /><br /> |
| − | Der Beweis kann direkt geführt werden, da er dem Beweis der Eindeutigkeit des Mittelpunktes nachgeht. Nehmen wir aber dennoch an, es gibt eine zweite Spiegelgerade f, mit f<math>\neq</math> g.
| |
| − | <br />
| |
| − | <br />
| |
| − | Es seien P ein Punkt und P' das Bild des Punktes P. P' entstand durch Spiegelung an g.<br />
| |
| − | Der Schnittpunkt von <math>g \cap \overline{PP'} </math> sei L.<br /><br />
| |
| − | Nach der Definition der Geradenspiegelung (bzw. Bild eines Punktes bei der Spiegelung) ist nun L Mittelpunkt von <math> \overline{PP'} </math>.<br />
| |
| − | Da der Mittelpunkt einer Strecke eindeutig ist, muss nun gelten, dass f ebenfalls durch L verläuft und senkrecht ist. Da aber nach dem Winkelkonstruktionsaxiom nur ein Winkel mit dem Maß 90 existiert, muss f <math>\equiv</math> g sein, was ein Widerspruch zu unserer Annahme ist. --[[Benutzer:HecklF|Flo60]] 21:29, 31. Okt. 2011 (CET)
| |
| | | | |
| | ==== Satz 2.3 ==== | | ==== Satz 2.3 ==== |
Leider sind meine Bilder von der Qualität her zu schlecht geworden, als dass sie hier veröffentlicht werden könnten. Wer hilft?
--*m.g.* 13:04, 27. Okt. 2011 (CEST)
Bemerkung zum Nachweis der Korrektheit des jeweiligen Schrittes: Gemeint ist eine Begründung, aus der hervorgeht, dass der jeweilige Schritt (ggf. eindeutig) ausführbar ist.










 bei einer Spiegelung an der Geraden
bei einer Spiegelung an der Geraden 
 ein Punkt der Ebene der nicht zur Geraden
ein Punkt der Ebene der nicht zur Geraden  dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von
dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von  bei der Spiegelung an
bei der Spiegelung an  . Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
. Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
 )
) eine Gerade. Unter der Spiegelung
eine Gerade. Unter der Spiegelung 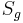 an der Geraden
an der Geraden  versteht man eine Abbildung der Ebene auf sich, ...
versteht man eine Abbildung der Ebene auf sich, ...
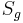 ist eine abstandserhaltende Abbildung.
ist eine abstandserhaltende Abbildung.
 ,
,  zwei Punkte, die an einer Geraden
zwei Punkte, die an einer Geraden  auf ihre Bilder
auf ihre Bilder 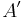 und
und 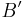 gespiegelt werden.
gespiegelt werden.


 ,
, 
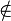


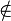
 ,
,  und
und  liegen in derselben Halbebene bezüglich
liegen in derselben Halbebene bezüglich 

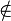
 ,
,  und
und  liegen in verschiedenen Halbebenen bezüglich
liegen in verschiedenen Halbebenen bezüglich 
 ist durch die Angabe eines Punktes
ist durch die Angabe eines Punktes  und dem Bild von
und dem Bild von 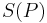 eindeutig bestimmt, falls
eindeutig bestimmt, falls 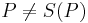 gilt.
gilt.