Version vom 14. Juni 2010, 13:59 Uhr

Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.

Wir formulieren Satz I neu und beginnen mit „Es seien $A$ , $B$ und $C$ drei Punkte.“ Ergänzen Sie: „Wenn $A$ , $B$ und $C$ … , dann … .“
Beweisen Sie Satz I indirekt.
Bilden Sie die Kontraposition von Satz I.
Beweisen Sie auch die Kontraposition von Satz I.
Formulieren Sie die Umkehrung von Satz I.
Gilt auch die Umkehrung von Satz I?

Lösung: --m.g. 12:41, 14. Jun. 2010 (UTC)

Teilaufgabe 1

Es seien $\ A$ , $\ B$ und $\ C$ drei Punkte.

Wenn $\ A$ , $\ B$ und $\ C$ kollinear sind , dann sind je zwei der Punkte $\ A$ , $\ B$ und $\ C$ nicht identisch.
Andere Formulierung: 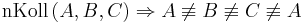$\operatorname{nKoll} \left( A, B, C \right) \Rightarrow A \not\equiv B \not\equiv C \not\equiv A$

Teilaufgabe 2: Indirekter Beweis der Implikation

Beweisprinzip

Wir nehmen an, dass bei wahrer Voraussetzung die Behauptung nicht gilt. Anders ausgedrückt: Wir negieren die Behauptung, bleiben aber dabei, dass die Voraussetzung wahr ist.

Bemerkung nebenbei: Es wäre sinnvoll, wenn sowas in Ihrem Glossar stehen würde. Dann bräuchte man jeweils nur einen Link zu setzen.

Voraussetzungen

allgemeine Voraussetzung

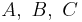$\ A, \ B, \ C$ sind drei Punkte

Bemerkung: Diese Voraussetzung möge ab sofort allem, was wir hier formulieren vorangestellt sein. Um uns auf das Wesentliche konzentrieren zu können, werden wir diese Voraussetzung nicht mehr explizit erwähnen.

spezielle Voraussetzung

Die drei Punkte 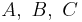$\ A, \ B, \ C$ sind nicht kollinear.

Andere Formulierungen:

Es gibt keine Gerade, die alle drei Punkte 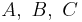$\ A, \ B, \ C$ enthält. (Übersetzung: nicht kollinear)
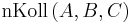
$\operatorname{nKoll} \left( A, B, C \right)$
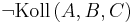
$\neg \operatorname{Koll} \left( A, B, C \right)$
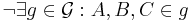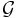$\neg \exists g \in \mathcal{G} : A, B, C \in g$ ( $\mathcal{G}$ sei die Menge aller Geraden unserer Theorie)
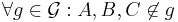
$\forall g \in \mathcal{G} : A,B, C \not\in g$

Behauptung

Je zwei der drei Punkte $\ A, B, C$ sind nicht identisch.

Andere Formulierungen:

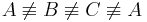$\ A \not\equiv B \not\equiv C \not\equiv A$ (Überlegen Sie, warum einer der drei Punkte hier zweimal genannt werden muss.)
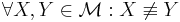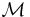$\forall X, Y \in \mathcal{M} : X \not\equiv Y$ ( $\mathcal{M}$ sei die Menge der Punkte $\ A, B, C$ )
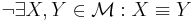
$\neg \exist X, Y \in \mathcal{M} : X \equiv Y$

Negation der Behauptung

Zwei der Punkte $\ A, B, C$ sind identisch.

Andere Formulierungen:

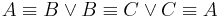$\ A \equiv B \or B \equiv C \or C \equiv A$ (Überlegen Sie, warum hier 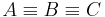$\ A \equiv B \equiv C$ enthalten ist.
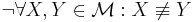
$\neg \forall X, Y \in \mathcal{M} : X \not\equiv Y$
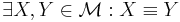
$\exist X, Y \in \mathcal{M} : X \equiv Y$

(3) noch mal in Worten:
Es gibt zwei Punkte aus der Menge der Punkte $\ A, B, C$ , die identisch sind.

Annahme für den indirekten Beweis

Es gibt zwei Punkte aus der Menge der Punkte $\ A, B, C$ , die identisch sind.

O.B.d.A. seien dieses die beiden Punkte $\ A$ und $\ B$ .

also Annahme:
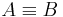
$\ A \equiv B$

Beweis

Fall 1

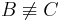
(*) $\ B \not\equiv C$

Nr.	Beweisschritt	Begründung
(i)	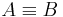$\ A \equiv B$	Annahme
(ii)	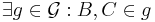$\exist g \in \mathcal{G}: B, C \in g$	Axiom I.1 und (*)
(iii)	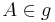$\ A \in g$	(i) und (ii)
(iv)	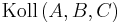$\operatorname{Koll} \left( A, B, C \right)$	(ii) und (iii)

Fall 2

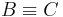(**) $\ B \equiv C$ , also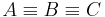 $\ A \equiv B \equiv C$

Nr.	Beweisschritt	Begründung
(o)	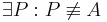$\exist P : P \not\equiv A$	Axiom I.3
(i)	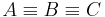$\ A \equiv B \equiv C$	Annahme (**)
(ii)	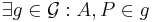$\exist g \in \mathcal{G}: A, P \in g$	Axiom I.1 und (i)
(iii)	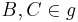$\ B, C \in g$	(i) und (ii)
(iv)	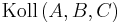$\operatorname{Koll} \left( A, B, C \right)$	(ii) und (iii)

(iv) ist ein Widerspruch zur Voraussetzung 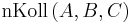$\operatorname{nKoll} \left( A,B, C \right)$

Die Annahme ist deshalb zu verwerfen.

Teilaufgabe 3

Kontraposition

Wenn nicht gilt: von drei Punkten sind je zwei nicht identisch, dann sind die drei Punkte nicht nicht kollinear.

Wir schmeißen die doppelten Verneinungen raus:

Wenn von drei Punkten zwei identisch sind, so sind die drei Punkte kollinear.

Teilaufgabe 4

Beweis der Kontraposition

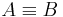
Voraussetzung: Von drei Punkte $\ A, B, C$ sind zwei identisch: o.B.d.A. $\ A \equiv B$

Behauptung: 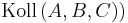$\operatorname{Koll} \left( A, B, C) \right)$

Fall 1: 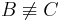$\ B \not\equiv C$

Fall 2: 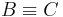$\ B \equiv C$

Jetzt geht es weiter wie in den beiden Fällen des indirekten Beweises, ohne dass wir auf einen Widerspruch kommen.
Erkennen Sie den Zusammenhang zwischen dem indirekten Beweisen einer Implikation und dem Beweisen ihrer Kontraposition?

Teilaufgabe 5

Die Umkehrung des Satzes

Wenn drei Punkte paarweise verschieden sind, dann sind sie nicht kollinear.

Teilaufgabe 6

Gültigkeit der Umkehrung

Gilt natürlich nicht. Beweis???

vorangegangene Diskussionen bzw. Lösungsvorschläge

1. Es seien $A$ , $B$ und $C$ drei Punkte. Wenn $A$ , $B$ und $C$ nicht kollinear sind , dann sind sie paarweise verschieden.
2. Voraussetzung: Es seien $A$ , $B$ und $C$ drei Punkte mit nkoll( $A$ , $B$ , $C$ ).
Annahme: $A$ identisch $B$ o.B.d.A.

Schritt	Begründung
1) Durch die Punkte $B$ und $C$ geht genau eine Gerade g. 2) $A$ identisch $B$ => $A$ Element g 3) $A$ Element g => koll( $A$ , $B$ , $C$ ) 4) Widerspruch zur Voraussetzung	1) Axiom I/1 2) Identität 3) Definition: (kollinear)

Bemerkungen von --*m.g.* 12:43, 14. Jun. 2010 (UTC):

Prinzipiell ist der Beweis ok.
Es fehlt allerdings der Fall, dass alle drei Punkte identisch sind.
Feintuning:

besser: Es gibt eine Gerade $\ g$ zu der die beiden Punkte ...; bei der Begründung darauf verweisen, dass $\ B$ und $\ C$ nicht identisch sind, denn nur dann kann man ja Axiom I.1 anwenden
Bei der Begründung auch darauf verweisen, dass $\ B$ auf der Geraden liegt, also zusätzlich mit Schritt (1) begründen.
Die eigentlichen Begründungen sind (1) und (3)

3. Sind drei Punkte nicht paarweise verschieden, so sind sie kollinear. korrekt --*m.g.* 12:55, 14. Jun. 2010 (UTC)
5. Sind drei Punkte paarweise verschieden, so sind sie nicht kollinear. korrekt --*m.g.* 12:55, 14. Jun. 2010 (UTC)
6. Nein. korrekt --*m.g.* 12:55, 14. Jun. 2010 (UTC)

4. Voraussetzung: $A$ , $B$ und $C$ sind nicht paarweise verschieden.
Annahme: nkoll ( $A$ , $B$ , $C$ )
I. durch die Punkte $A$ und $C$ geht genau eine Gerade g. ->Axiom I/1
II. $B$ ist kein Element von g -> Annahme
III. $B$ nicht identisch $A$ und $B$ nicht identisch $C$ -> I. und II.
IV. Widerspruch zur Voraussetzung

Bemerkungen von --*m.g.* 12:59, 14. Jun. 2010 (UTC): der Beweis ist schief gegangen

@@ Zeile 182: / Zeile 182: @@
 III. <math>B</math> nicht identisch <math>A</math> und <math>B</math> nicht identisch <math>C</math> -> I. und II. <br />
 IV. Widerspruch zur Voraussetzung
+Bemerkungen von --[[Benutzer:*m.g.*|*m.g.*]] 12:59, 14. Jun. 2010 (UTC):
+der Beweis ist schief gegangen

Lösung von Aufgabe 4: Unterschied zwischen den Versionen

Version vom 14. Juni 2010, 13:59 Uhr

Inhaltsverzeichnis

Lösung: --m.g. 12:41, 14. Jun. 2010 (UTC)

Teilaufgabe 1