Lösung von Zusatzaufgabe 6.1P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 13: | Zeile 13: | ||
!Beweisschritt!!Begründung | !Beweisschritt!!Begründung | ||
|- | |- | ||
| − | | 1 |AB| + |BC| = |AC| || Voraussetzung, Def. Zwischenrelation | + | | 1 <math>|AB| + |BC| = |AC|</math> || Voraussetzung, Def. Zwischenrelation |
|- | |- | ||
| 2 <math>B \in \overline{AC} </math> || 1.) | | 2 <math>B \in \overline{AC} </math> || 1.) | ||
Version vom 17. Januar 2013, 22:36 Uhr
Beweisen Sie: Aus  folgt
folgt  .
.
Zum Verwenden von mathematischen Zeichen, kann man den Formeleditor öffnen (Symbol ganz links, Summenzeichen). Als Hilfestellung schon mal eine Tabelle. --Tutorin Anne 12:38, 10. Dez. 2012 (CET)
| Voraussetzung | Zw (A,B,C) |
| Behauptung | koll (A,B,C) |
| Beweisschritt | Begründung |
|---|---|
1 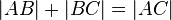 |
Voraussetzung, Def. Zwischenrelation |
2 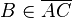 |
1.) |
3 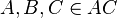 |
1,) ; 2,) |
| 4 koll (A,B,C) | 3.); Def. koll |
Ich bin mir aber nicht sicher, ob man das so machen kann, kommt mir irgendwie zu primitiv vor...--Unicycle 22:13, 17. Jan. 2013 (CET)

