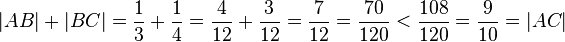Probeklausur WS 12 13 Aufgabe 2: Unterschied zwischen den Versionen
(→Aufgabe b) |
B..... (Diskussion | Beiträge) (→Bemerkung --*m.g.* 12:34, 11. Feb. 2013 (CET)) |
||
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| − | + | <br />Da alle Seiten laut der Vorraussetzung kongruent sind, sind laut dem Basiswinkelsatz auch alle Innenwinkel kongruent.--[[Benutzer:B.....|B.....]] 14:16, 5. Feb. 2013 (CET) | |
==Lösung User ...== | ==Lösung User ...== | ||
| Zeile 22: | Zeile 22: | ||
==Lösung User ...lw)...== | ==Lösung User ...lw)...== | ||
Mittelsenkrechtenkriterium | Mittelsenkrechtenkriterium | ||
| + | |||
| + | schwacher Außenwinkelsatz--LilPonsho 11:43, 5. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
| + | <br /> | ||
| + | da es nur um die Eindeutigkeit des Lotes geht reicht der Außenwinkelsatz.--[[Benutzer:B.....|B.....]] 14:19, 5. Feb. 2013 (CET) | ||
=Aufgabe c= | =Aufgabe c= | ||
| Zeile 32: | Zeile 36: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| − | + | <br />Vor.: Dreieck OLP<br /> Laut Def. Lot, Lotgerade, Lotfußpunkt ist der Winkel OLP = 90.<br /> | |
| + | Laut Def. Innenwinkelsumme ist der Winkel LPO = 45.<br /> | ||
| + | Laut der Umkehrung des Basiswinkelsatzes ist somit das Dreieck OPL gleichschenklig--[[Benutzer:B.....|B.....]] 14:22, 5. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
| Zeile 42: | Zeile 48: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| + | <br /> | ||
| + | Ann.: b ist kleiner gleich a<br /> | ||
| + | Fall 1: b ist kleiner als a<br /> | ||
| + | Widerspruch zur Vor. des schon bewiesenen Teils.<br /><br /> | ||
| + | Fall 2: b ist gleich a<br /> | ||
| + | laut dem Basiswinkelsatz sind dann auch die Winkel alpha und beta gleich groß.<br /> | ||
| + | Ist ist ein Widerspruch zur Vorraussetzung.<br /> | ||
| + | Somit ist die Annahme zu verwerfen. | ||
==Lösung User ...== | ==Lösung User ...== | ||
| Zeile 52: | Zeile 66: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| + | <br /> | ||
| + | laut Vor.:<br />AB=0,9<br /> BC=2,7<br />AC=3,6<br /> | ||
| + | daraus folgt: AB+BC=AC<br /> | ||
| + | Nach dem Axiom II/3 (Dreiecksungleichung) sind die Punkte kollinear<br />koll(A,B,C)<br /><br /> | ||
| + | Somit ist nach Definition Dreieck zu folgern, dass das Dreieck ABC nicht existiert.--[[Benutzer:B.....|B.....]] 14:31, 5. Feb. 2013 (CET) | ||
| + | ===Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 12:34, 11. Feb. 2013 (CET)=== | ||
| + | Wie kommen Sie auf diese merkwürdige Rechnung?<br /> | ||
| + | <math>|AB|+|BC|=\frac{1}{3}+\frac{1}{4}=\frac{4}{12}+\frac{3}{12}=\frac{7}{12}= \frac{70}{120}<\frac{108}{120}=\frac{9}{10}=|AC|</math><br /> | ||
| + | <br /> | ||
| + | oh - ich dachte es wäre 1/3 mal BC. Habe nicht erkannt dass es ein Komma ist.--[[Benutzer:B.....|B.....]] 20:27, 11. Feb. 2013 (CET) | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 11. Februar 2013, 20:27 Uhr
|
Aufgabe aBegründen Sie kurz und knapp, warum im gleichseitigen Dreieck alle Winkel zueinander kongruent sind.
Lösung User ...
Lösung User ...Aufgabe bWelcher Satz ist unabdingbar für den Beweis der Eindeutigkeit des Lotes von einem Punkt auf eine Gerade im Rahmen der absoluten Geometrie?
Lösung User ...lw)...Mittelsenkrechtenkriterium schwacher Außenwinkelsatz--LilPonsho 11:43, 5. Feb. 2013 (CET) Lösung User ...
Aufgabe cBezüglich eines kartesischen Koordinatensystems mit dem Ursprung
Lösung User ...
Lösung User ...Aufgabe dEs sei
Lösung User ...
Fall 1: b ist kleiner als a Lösung User ...Aufgabe eEs gelte:
Lösung User ...
Bemerkung --*m.g.* 12:34, 11. Feb. 2013 (CET)Wie kommen Sie auf diese merkwürdige Rechnung? Lösung User ... |
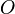 sei ein Einheitskreis
sei ein Einheitskreis  in Mittelpunktslage gegeben. Ferner seien
in Mittelpunktslage gegeben. Ferner seien 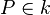 und
und 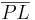 das Lot von
das Lot von  auf die
auf die 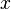 -Achse. Beweisen Sie unter Bezug auf eine Skizze in der Euklidischen Geometrie: Wenn
-Achse. Beweisen Sie unter Bezug auf eine Skizze in der Euklidischen Geometrie: Wenn 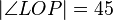 ° dann ist
° dann ist 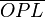 gleichschenklig.
gleichschenklig.
 ein Dreieck mit den schulüblichen Bezeichnungen. Es sei bereits gezeigt:
ein Dreieck mit den schulüblichen Bezeichnungen. Es sei bereits gezeigt: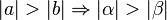 . Beweisen Sie in der absoluten Geometrie:
. Beweisen Sie in der absoluten Geometrie: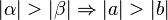 .
.
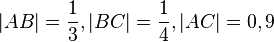 . Existiert
. Existiert