Lösung Aufgabe 1.08 soSe 2013: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung User ...) |
User m (Diskussion | Beiträge) (→Lösung User ...) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
=Lösung User ...= | =Lösung User ...= | ||
| − | Wenn | + | Wenn <math>\varepsilon_0</math> <math>K</math> schneidet, ohne dass <math>\varepsilon</math> geschnitten wird, dann ist der Schnitt von <math>\varepsilon_0</math> mit <math>K</math> eine Ellipse. --[[Benutzer:Bushaltefolie|Bushaltefolie]] 11:44, 14. Mai 2013 (CEST) |
=Lösung User ...= | =Lösung User ...= | ||
| − | + | Warum muss <math>\beta</math> < 90° - '''<math>\alpha/2</math>''' sein, bzw. wie komme ich auf <math>\alpha/2</math>? (siehe PDF mit Lösungen) <br /> | |
| + | Dass <math>\beta</math> kleiner 90° sein muss ist mir klar.<br /> | ||
| + | --[[Benutzer:User m|User m]] 11:59, 19. Mai 2013 (CEST) | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 19. Mai 2013, 10:59 Uhr
|
AufgabeEllipsen lassen sich auch als Kegelschnitte definieren. Es sei Definition Wenn ... , dann ist der Schnitt von Lösung User ...Wenn Lösung User ...Warum muss |
 ein Kegel mit dem Öffnungswinkel
ein Kegel mit dem Öffnungswinkel  und der Spitze
und der Spitze  . Seine Rotationsachse
. Seine Rotationsachse  möge senkrecht auf der Ebene
möge senkrecht auf der Ebene
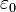 stehen. Es sei
stehen. Es sei  eine zweite Ebene, die
eine zweite Ebene, die  < 90° -
< 90° - 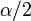 sein, bzw. wie komme ich auf
sein, bzw. wie komme ich auf 
