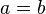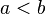Lösung von Aufgabe 4.06 S SoSe 13: Unterschied zwischen den Versionen
(→Lösung User ...) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 23:03, 3. Jun. 2013 (CEST)) |
||
| (7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
==Lösung User ...== | ==Lösung User ...== | ||
| − | Umkehrung: <math>\alpha > \beta | + | Umkehrung: <math>\alpha > \beta \Rightarrow a > b</math> <br /> |
<br /> | <br /> | ||
Vor.: <math>\alpha >\beta</math> <br /> | Vor.: <math>\alpha >\beta</math> <br /> | ||
| Zeile 20: | Zeile 20: | ||
(2) Hieraus folgt, dass <math>\alpha > \beta</math> und somit auch a > b sein muss, da beides immer die selbe Relation haben.<br /> | (2) Hieraus folgt, dass <math>\alpha > \beta</math> und somit auch a > b sein muss, da beides immer die selbe Relation haben.<br /> | ||
a > b ist ein Widerspruch zur Behauptung. | a > b ist ein Widerspruch zur Behauptung. | ||
| + | |||
| + | |||
| + | ===Bemerkung --[[Benutzer:*m.g.*|*m.g.*]] 23:03, 3. Jun. 2013 (CEST)=== | ||
| + | Ihre Behauptung ist falsch: Die zu beweisende Implikation lautet:<br /> | ||
| + | <math>\alpha > \beta \Rightarrow a > b</math> <br /> | ||
| + | Es wird also behauptet:<br /> | ||
| + | <math> a > b</math><br /> | ||
| + | |||
| + | Wahrscheinlich meinten Sie die Annahme (die Negation der Behauptung) Die Negation der Behauptung ist jedoch: | ||
| + | |||
| + | <math>a\leq b</math><br /> | ||
| + | |||
| + | Aus dem <math>\leq</math> resultieren die beiden Fallunterscheidungen: <br /> | ||
| + | (1) <math>a=b</math><br /> | ||
| + | (2) <math>a<b</math> | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 3. Juni 2013, 22:12 Uhr
Aufgabe 4.06Sie dürfen davon ausgehen, dass für jedes Dreieck gilt: Der größeren zweier Seiten liegt der größere Innenwinkel gegenüber. Lösung User ...Umkehrung: (1)Basiswinkelsatz:
Bemerkung --*m.g.* 23:03, 3. Jun. 2013 (CEST)Ihre Behauptung ist falsch: Die zu beweisende Implikation lautet: Wahrscheinlich meinten Sie die Annahme (die Negation der Behauptung) Die Negation der Behauptung ist jedoch:
Aus dem Lösung User ...Lösung User ...
|
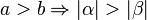 )
Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie diese Umkehrung mittels eines Widerspruchsbeweises.
)
Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie diese Umkehrung mittels eines Widerspruchsbeweises.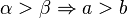
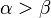
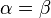
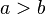
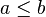
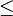 resultieren die beiden Fallunterscheidungen:
resultieren die beiden Fallunterscheidungen: