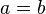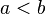Lösung von Aufgabe 4.06 S SoSe 13
Aufgabe 4.06Sie dürfen davon ausgehen, dass für jedes Dreieck gilt: Der größeren zweier Seiten liegt der größere Innenwinkel gegenüber. Lösung User ...Umkehrung: (1)Basiswinkelsatz:
Bemerkung --*m.g.* 23:03, 3. Jun. 2013 (CEST)Ihre Behauptung ist falsch: Die zu beweisende Implikation lautet: Wahrscheinlich meinten Sie die Annahme (die Negation der Behauptung) Die Negation der Behauptung ist jedoch:
Aus dem Lösung User ...Lösung User ...
|
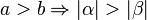 )
Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie diese Umkehrung mittels eines Widerspruchsbeweises.
)
Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie diese Umkehrung mittels eines Widerspruchsbeweises.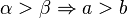
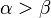
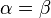
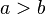
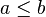
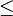 resultieren die beiden Fallunterscheidungen:
resultieren die beiden Fallunterscheidungen: