Serie 6 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 6.10) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 6.09) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
# Formulieren Sie Lenas "Definition" als Konventionaldefinition. | # Formulieren Sie Lenas "Definition" als Konventionaldefinition. | ||
| − | # Es ist klar, dass Lenas Definition nicht den formal korrekten | + | # Es ist klar, dass Lenas Definition nicht den formal korrekten Ansprüchen eines Mathematikers genügt. Aber auch im Sinne einer informellen Definition auf Schülerniveau wäre Lenas Definition verbesserunsgwürdig. Skizzieren Sie einen Denkanstoß, den Sie Lena geben würden, damit Sie selbst ihre Definition präzisieren kann. |
# Formulieren Sie eine verbesserte Variante von Lenas Definition. Bleiben Sie dabei auf dem Niveau einer informellen Definition. | # Formulieren Sie eine verbesserte Variante von Lenas Definition. Bleiben Sie dabei auf dem Niveau einer informellen Definition. | ||
| Zeile 78: | Zeile 78: | ||
<math>\left|P_{3,4}P_{5,1}\right|:=|3-5|+|4-1|=|-2|+|3|=5</math> | <math>\left|P_{3,4}P_{5,1}\right|:=|3-5|+|4-1|=|-2|+|3|=5</math> | ||
<br /> Untersuchen Sie, ob in dem Modell die Dreiecksungleichung erfüllt ist:<br /> | <br /> Untersuchen Sie, ob in dem Modell die Dreiecksungleichung erfüllt ist:<br /> | ||
| − | <math>\forall A,B,C \in \mathbb{P}: |AB|+|BC|\ | + | <math>\forall A,B,C \in \mathbb{P}: |AB|+|BC|\geq |AC|</math><br /><br /> |
[[Lösung von Aufgabe 6.09 S SoSe 13]] | [[Lösung von Aufgabe 6.09 S SoSe 13]] | ||
==Aufgabe 6.10== | ==Aufgabe 6.10== | ||
| − | Wir gehen von dem Modell aus Aufgabe 6.09 aus. Wir betrachten in diesem Modell (ebene Geometrie) einen Kreis <math>k</math> mit dem <math> | + | Wir gehen von dem Modell aus Aufgabe 6.09 aus. Wir betrachten in diesem Modell (ebene Geometrie) einen Kreis <math>k</math> mit dem Mittelpunkt <math>M:=P_{3,3}</math> und dem Radius <math>r=2</math>. Zählen Sie alle Punkte auf, die zu <math>k</math> gehören.<br /><br /> |
[[Lösung von Aufgabe 6.10 S SoSe 13]] | [[Lösung von Aufgabe 6.10 S SoSe 13]] | ||
<!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
Aktuelle Version vom 4. Juni 2013, 08:20 Uhr
|
Aufgabe 6.01Lena aus der 5a erklärt Ihnen, was eine Strecke ist: Strecken sind Teile von Geraden. Mein Papa hat mir gesagt, dass die Mathematiker nicht einfach so Teil sondern Teilmenge sagen. Und zu einer Festlegung sagen sie Definition. Ich definiere also:
Aufgabe 6.02Im Folgenden sind wieder formal korrekte Definitionen verlangt. Zur Verfügung steht Ihnen dazu nur die bisher aufgebaute axiomatische Theorie der Geometrie.
Aufgabe 6.03Definieren Sie den Begriff Halbgerade
Aufgabe 6.04Es seien Begründen Sie, warum die Zerlegung einer Geraden Aufgabe 6.05Es seien Lösung von Aufgabe 6.05 S SoSe 13 Aufgabe 6.06Wir befinden uns in der ebenen Geometrie. Aufgabe 6.07Zeigen Sie, dass für drei paarweise verschiedene Punkte Aufgabe 6.08Definition Zwei Geraden sind komplanar, wenn es eine Ebene gibt, die beide Geraden vollständig enthält. Beweisen Sie den folgenden Satz:
Aufgabe 6.09Wir betrachten die folgende Menge Aufgabe 6.10Wir gehen von dem Modell aus Aufgabe 6.09 aus. Wir betrachten in diesem Modell (ebene Geometrie) einen Kreis |
 und Halbgerade
und Halbgerade  .
.
 eine Menge und
eine Menge und 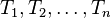 Teilmengen von
Teilmengen von 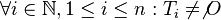
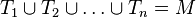
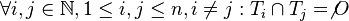
 in die Halbgeraden
in die Halbgeraden  ,
,  und
und  drei paarweise verschiedene kollineare Punkte. Beweisen Sie, dass genau einer dieser drei Punkte zwischen den anderen beiden dieser drei Punkte liegt.
drei paarweise verschiedene kollineare Punkte. Beweisen Sie, dass genau einer dieser drei Punkte zwischen den anderen beiden dieser drei Punkte liegt.
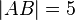 .
. 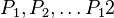 , für die gilt:
, für die gilt: 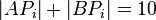 ,
, 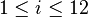 .
.  und
und  gilt:
gilt: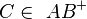 und
und 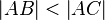 dann gilt
dann gilt 
 und
und  genau einen Schnittpunkt haben, so sind sie komplanar.
genau einen Schnittpunkt haben, so sind sie komplanar.
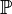 von Modellpunkten:
von Modellpunkten: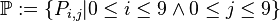 .
.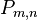 und
und 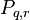 :
: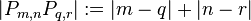
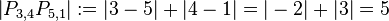
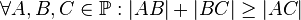
 mit dem Mittelpunkt
mit dem Mittelpunkt 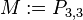 und dem Radius
und dem Radius 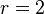 . Zählen Sie alle Punkte auf, die zu
. Zählen Sie alle Punkte auf, die zu 
