Lösung von Aufgabe 8.1P (SoSe 13): Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
*... | *... | ||
| − | |||
| + | |||
| + | |||
| + | [[Datei:feuerwehr.png|400px]] | ||
| + | |||
| + | <br /> | ||
| + | Wer macht sich die Mühe und schreibt eine Konstruktionsanleitung oder stellt seine Konstruktion ein? Vorallem das genaue Beschreiben und Begründen seiner Konstruktion ist eine super Übung.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:22, 26. Jun. 2013 (CEST)<br /> | ||
| + | |||
| + | Ich habe mal versucht, eine Beschreibung aufzuschreiben. BIN MIR ABER NICHT SICHER, OB ES RICHTIG IST. HILFE!<br /> | ||
'''Mögliche Konstruktionsbeschreibung'''[[Link-Text]] | '''Mögliche Konstruktionsbeschreibung'''[[Link-Text]] | ||
| Zeile 13: | Zeile 20: | ||
Ges.: Konstruktionsbeschreibung bzw. Minimale Weg für Punkt A um Punkt B zu erreichen | Ges.: Konstruktionsbeschreibung bzw. Minimale Weg für Punkt A um Punkt B zu erreichen | ||
| − | 1. Spiegele den Punkt A an g ( es entsteht A`) | + | 1. Spiegele den Punkt A an g ( es entsteht A`)<br /> |
2. Verbinde die Punkte BSA` zu einer Gerade. Punkt A und B liegen in der selben Halbebenen, daraus folgt, dass die Strecke AA´auch Punkt S in g schneidet (Längentreue) | 2. Verbinde die Punkte BSA` zu einer Gerade. Punkt A und B liegen in der selben Halbebenen, daraus folgt, dass die Strecke AA´auch Punkt S in g schneidet (Längentreue) | ||
| Zeile 19: | Zeile 26: | ||
3. Länge AS und Länge BS mit einer Geraden verbinden | 3. Länge AS und Länge BS mit einer Geraden verbinden | ||
| − | --> Es gilt: Länge der Strecken AS und BS ist minimal, wenn koll(BSA´)--[[Benutzer:Blumenkind|Blumenkind]] 15:16, 30. Jun. 2013 ( | + | --> Es gilt: Länge der Strecken AS und BS ist minimal, wenn koll(BSA´)--[[Benutzer:Blumenkind|Blumenkind]] 15:16, 30. Jun. 2013 <br /><br /> |
| − | + | Deine Konstruktionsbeschreibung ist schon ganz gut. Besser ist es, wenn du S nicht unter "Gegeben" nennst, da der Punkt sonst dadurch festgelegt ist. Im Nachhinein (Schritt 2) kannst du dann nicht mehr davon ausgehen, dass B, S, A' auf einer Geraden lieben. Stattdessen musst du S erst in Schritt 2 bennenen als Schnittpunkt der Gerade BA' und der Gerade g. <br /> | |
| − | + | Dein "daraus folgt"Schritt mit "wenn koll(BSA')" ist nicht logisch, wenn du in Schritt 2 schon davon sprichst, dass die Punkte auf einer Geraden liegen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 15:40, 30. Jun. 2013 (CEST) | |
| − | + | ||
| − | <br /> | + | |
| − | + | ||
<br /> | <br /> | ||
[[Kategorie: Einführung_P]] | [[Kategorie: Einführung_P]] | ||
Version vom 30. Juni 2013, 14:40 Uhr
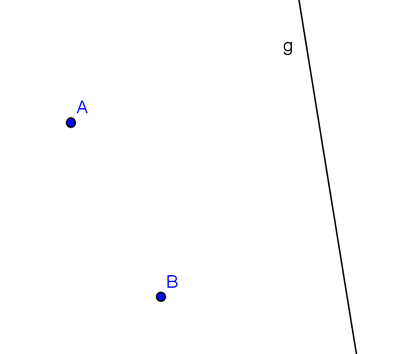
Das klassische Feuerwehrproblem: Am Punkt A steht die Feuerwehr, Punkt B symbolisiert das brennende Haus. Die Gerade g ist die Uferbegrenzung eines Flusses, aus dem die Feuerwehr das Wasser holen muss. Welchen Weg muss die Feuerwehr nehmen um Löschwasser am Fluss zu tanken um danach möglichst schnell am brennenden Haus zu sein? Konstruieren Sie nachstehend die optimale Route für die Feuerwehr und begründen Sie Ihre Konstruktion.
Das Problem lässt sich auf viele verschiedene Anwendungen übertragen, z. B.:
- reitende Cowboys, die ihr Pferd noch tränken müssen, bevor sie den Salon in Doce City erreichen
- Lichtstrahlen, die am Spiegel g reflektiert werden und immer den kürzesten Weg nehmen
- Billardkugeln, die durch einen zentralen Stoß und über Bande g einander treffen sollen
- ...
Wer macht sich die Mühe und schreibt eine Konstruktionsanleitung oder stellt seine Konstruktion ein? Vorallem das genaue Beschreiben und Begründen seiner Konstruktion ist eine super Übung.--Tutorin Anne 15:22, 26. Jun. 2013 (CEST)
Ich habe mal versucht, eine Beschreibung aufzuschreiben. BIN MIR ABER NICHT SICHER, OB ES RICHTIG IST. HILFE!
Mögliche KonstruktionsbeschreibungLink-Text
Geg: Punkt A ( steht für Feuerwehr), Punkt B (steht für Haus), Gerade g (Uferbegrenzung) und Punkt S mit S ist Element g.
Ges.: Konstruktionsbeschreibung bzw. Minimale Weg für Punkt A um Punkt B zu erreichen
1. Spiegele den Punkt A an g ( es entsteht A`)
2. Verbinde die Punkte BSA` zu einer Gerade. Punkt A und B liegen in der selben Halbebenen, daraus folgt, dass die Strecke AA´auch Punkt S in g schneidet (Längentreue)
3. Länge AS und Länge BS mit einer Geraden verbinden
--> Es gilt: Länge der Strecken AS und BS ist minimal, wenn koll(BSA´)--Blumenkind 15:16, 30. Jun. 2013
Deine Konstruktionsbeschreibung ist schon ganz gut. Besser ist es, wenn du S nicht unter "Gegeben" nennst, da der Punkt sonst dadurch festgelegt ist. Im Nachhinein (Schritt 2) kannst du dann nicht mehr davon ausgehen, dass B, S, A' auf einer Geraden lieben. Stattdessen musst du S erst in Schritt 2 bennenen als Schnittpunkt der Gerade BA' und der Gerade g.
Dein "daraus folgt"Schritt mit "wenn koll(BSA')" ist nicht logisch, wenn du in Schritt 2 schon davon sprichst, dass die Punkte auf einer Geraden liegen.--Tutorin Anne 15:40, 30. Jun. 2013 (CEST)