Der Basiswinkelsatz SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Satz VIII.1: (Basiswinkelsatz)) |
(→Satz VIII.1: (Basiswinkelsatz)) |
||
| Zeile 23: | Zeile 23: | ||
| [[Bild:gleichschenklig_2.png| 200 px]] | | [[Bild:gleichschenklig_2.png| 200 px]] | ||
| <math>\left| AC \right|=\left| BC \right|</math> | | <math>\left| AC \right|=\left| BC \right|</math> | ||
| − | | Voraussetzung | + | | Voraussetzung --[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:36, 2. Jul. 2013 (CEST) |
|- | |- | ||
| (2) | | (2) | ||
Version vom 2. Juli 2013, 11:36 Uhr
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VIII.1 : (gleichschenkliges Dreieck)
Das können sie selbst. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.
Übungsaufgabe
Der Basiswinkelsatz
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
Behauptung: Die Basiswinkel sind kongruent zueinander: |α| = |β| --Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 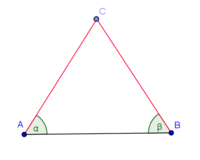
|
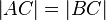
|
Voraussetzung --Nolessonlearned 12:36, 2. Jul. 2013 (CEST) |
| (2) | 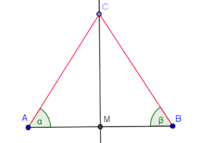
|
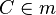 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
Begründung? |
| (3) | |
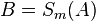
|
Begründung? |
| (4) | |
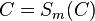
|
Begründung? |
| (5) | |
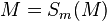
|
Begründung? |
| (6) | |
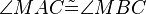
|
Begründung? |

