Lösung von Aufgabe 10.2P (SoSe 13): Unterschied zwischen den Versionen
(→Satz VIII.1: (Basiswinkelsatz)) |
|||
| Zeile 4: | Zeile 4: | ||
::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /><br /> | ::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /><br /> | ||
| − | |||
| − | |||
Beweis:<br /> | Beweis:<br /> | ||
| Zeile 49: | Zeile 47: | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | <br /> | ||
| + | Ich habe den Beweis selbst versucht: <br /> | ||
| + | [[Datei:IMG 0002.jpg|| 700px]]--[[Benutzer:Regenschirm|Regenschirm]] 18:00, 2. Jul. 2013 (CEST) | ||
| + | Der Beweis ist korrekt. Ich würde die Begründungen für Schritt 1 und 6 noch ergänzen.<br /> | ||
| + | Allerdings hast du nicht die Abbildungsgeometrie genutzt sondern bist über den Kongruenzsatz SSW gegangen. So wie wir hier die Geometrie aufbauen (Abbildungsgeometrisch eben), haben wir diese Kongruenzsätze aber noch nicht bewiesen und genau genommen, hast du die Aufgabe damit nicht erfüllt (da nicht abbildungsgeometrisch bewiesen).--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:37, 3. Jul. 2013 (CEST) | ||
Version vom 3. Juli 2013, 09:37 Uhr
Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
Behauptung: Die Basiswinkel sind kongruent zueinander: |α| = |β| --Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 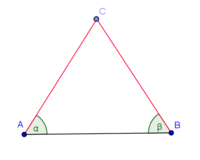
|
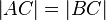
|
Voraussetzung --Nolessonlearned 12:36, 2. Jul. 2013 (CEST) |
| (2) | 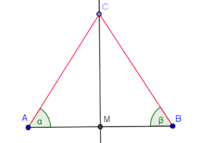
|
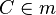 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
(1); Mittelsenkrechtenkriterium --Nolessonlearned 12:37, 2. Jul. 2013 (CEST) |
| (3) | |
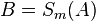
|
Streckentreue bzw Abstanderhaltung der Geradenspiegelung --Nolessonlearned 12:48, 2. Jul. 2013 (CEST) |
| (4) | |
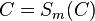
|
C∈m mit m:= Spiegelachse ⇒ C ist Fixpunkt--Nolessonlearned 12:51, 2. Jul. 2013 (CEST) |
| (5) | |
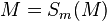
|
M∈m mit m:= Spiegelachse ⇒ M ist Fixpunkt--Nolessonlearned 12:53, 2. Jul. 2013 (CEST) |
| (6) | |
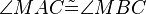
|
Winkeltreue der Geradenspiegelung--Nolessonlearned 12:57, 2. Jul. 2013 (CEST) |
Ich habe den Beweis selbst versucht:
 --Regenschirm 18:00, 2. Jul. 2013 (CEST)
Der Beweis ist korrekt. Ich würde die Begründungen für Schritt 1 und 6 noch ergänzen.
--Regenschirm 18:00, 2. Jul. 2013 (CEST)
Der Beweis ist korrekt. Ich würde die Begründungen für Schritt 1 und 6 noch ergänzen.
Allerdings hast du nicht die Abbildungsgeometrie genutzt sondern bist über den Kongruenzsatz SSW gegangen. So wie wir hier die Geometrie aufbauen (Abbildungsgeometrisch eben), haben wir diese Kongruenzsätze aber noch nicht bewiesen und genau genommen, hast du die Aufgabe damit nicht erfüllt (da nicht abbildungsgeometrisch bewiesen).--Tutorin Anne 10:37, 3. Jul. 2013 (CEST)

