Lösung von Aufgabe 11.2P (SoSe 13): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.<br /> [[Kategorie:Ei…“) |
|||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.<br /> | Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.<br /> | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| + | |||
| + | Umkehrsatz: Wenn Wechselwinkel an g und h kongruent sind, dann sind g und h parallel zueinander. | ||
| + | |||
| + | Vor.: <math>\alpha \tilde {=} \beta</math> | ||
| + | |||
| + | Beh.: gIIh | ||
| + | |||
| + | Anmerkung: Ich habe mir eine Skizze gezeichnet: 2 Geraden a und b, die von einer dritten Geraden geschnitten wird mit a geschnitten c = H und b geschnitten c= G, sowie Punkt A ist Element a und A' ist Element b (gehört alles zur Voraussetzung)<br /> | ||
| + | [[Datei:Übung_11-2-Skizze1.PNG]] >nach Schritt 2 > [[Datei:Übung_11-2-Skizze2.PNG]]--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:30, 12. Jul. 2013 (CEST) | ||
| + | Ich habe die Winkelbezeichnungen geändert, da ich sie in meiner Skizze anders versehentlich anders benannt habe. <br /> | ||
| + | Beweis:<br /> | ||
| + | 1) Punkt S ist Mittelpunkt von der Strecke GH ( IGSI = ISHI) ;Def. Mittelpunkt<br /> | ||
| + | 2) <math>\alpha</math> = <A'GS und <math>\beta</math> = <SHA ; (1), VORAUSSETZUNG<br /> | ||
| + | |||
| + | 3) D (S,180) <A'GS = <SHA <br /> Def. Punktspiegelung | ||
| + | wenn du neue Namen in 2) einfüge, dann nutze sie auch: D (S,180)<math>\alpha</math> = <math>\beta</math> <br /> | ||
| + | Außerdem: Die Begründung ist hier nicht ausreichend.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:30, 12. Jul. 2013 (CEST) | ||
| + | 4) GA'+ II HA+ ; Eigenschaft Punktspiegelung, (3), <s>Winkelmaßerhaltung, Winkeltreue </s> <br /> | ||
| + | Folgt aus einer weitern Eigenschaften der Punktspiegelung. Welche?--[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:30, 12. Jul. 2013 (CEST) | ||
| + | 5) aIIb; 4 | ||
| + | --[[Benutzer:Blumenkind|Blumenkind]] 10:50, 12. Jul. 2013 (CEST)Blumenkind 10:49, 12. Juli | ||
| + | Wenn die angemerkten Dinge noch ergänzt/ korrigiert werden, stimmt der Beweis. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 16:30, 12. Jul. 2013 (CEST) | ||
Aktuelle Version vom 12. Juli 2013, 16:34 Uhr
Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.
Umkehrsatz: Wenn Wechselwinkel an g und h kongruent sind, dann sind g und h parallel zueinander.
Vor.: 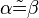
Beh.: gIIh
Anmerkung: Ich habe mir eine Skizze gezeichnet: 2 Geraden a und b, die von einer dritten Geraden geschnitten wird mit a geschnitten c = H und b geschnitten c= G, sowie Punkt A ist Element a und A' ist Element b (gehört alles zur Voraussetzung)
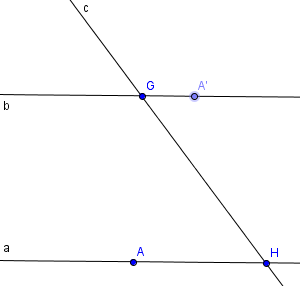
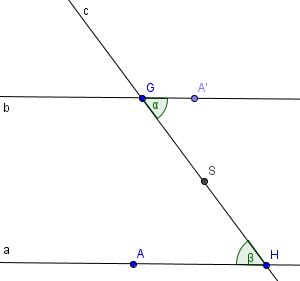
Ich habe die Winkelbezeichnungen geändert, da ich sie in meiner Skizze anders versehentlich anders benannt habe.
Beweis:
1) Punkt S ist Mittelpunkt von der Strecke GH ( IGSI = ISHI) ;Def. Mittelpunkt
2)  = <A'GS und
= <A'GS und  = <SHA ; (1), VORAUSSETZUNG
= <SHA ; (1), VORAUSSETZUNG
3) D (S,180) <A'GS = <SHA
Def. Punktspiegelung
wenn du neue Namen in 2) einfüge, dann nutze sie auch: D (S,180)=

Außerdem: Die Begründung ist hier nicht ausreichend.--Tutorin Anne 16:30, 12. Jul. 2013 (CEST)
4) GA'+ II HA+ ; Eigenschaft Punktspiegelung, (3), Winkelmaßerhaltung, Winkeltreue
Folgt aus einer weitern Eigenschaften der Punktspiegelung. Welche?--Tutorin Anne 16:30, 12. Jul. 2013 (CEST)
5) aIIb; 4 --Blumenkind 10:50, 12. Jul. 2013 (CEST)Blumenkind 10:49, 12. Juli
Wenn die angemerkten Dinge noch ergänzt/ korrigiert werden, stimmt der Beweis. --Tutorin Anne 16:30, 12. Jul. 2013 (CEST)

