Wir waren auf den Königsstuhl SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Der Berg wurde schon mal bezwungen) |
*m.g.* (Diskussion | Beiträge) (→Sätze am Kreis sind für die Klausur relevant) |
||
| (16 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | <!--- ------------------------------------------------------------------------------------------ ---> | ||
=Der Berg wurde schon mal bezwungen= | =Der Berg wurde schon mal bezwungen= | ||
| Zeile 15: | Zeile 20: | ||
|- | |- | ||
|Der Lohn der Mühen: || Wahnsinnsausblick | |Der Lohn der Mühen: || Wahnsinnsausblick | ||
| + | |- | ||
| + | | [[Datei:WP 20130714 031.jpg|400px]] || [[Datei:WP 20130714 033.jpg|400px]] | ||
| + | |- | ||
| + | |Sowas gibt es nur an der PH HD: || Mathematik auf dem Königsstuhl | ||
|} | |} | ||
| + | =Was passierte auf dem Königsstuhl?= | ||
| + | ==Tips zur Vorbereitung auf die Klausur== | ||
| + | ===Inhaltlich=== | ||
| + | ====Faltkonstruktion eines Parallelogramms==== | ||
| + | Es sei <math>P:=\overline{ABCD}</math> ein weißes Blatt Papier im Format DIN A4. Wie faltet man mit <math>P</math> ein Parallelogramm, wenn man die Seiten <math>\overline{AB}, \overline{BC}, \overline{CD}, \overline{DA}</math> in keiner Art und Weise für die Faltkonstruktion verwenden darf? | ||
| + | ====Beweisen wie die Schüler==== | ||
| + | Die Anzahl der Punkte, die es für jeden Schritt des Beweises gibt, ist gleichzeitig ein Hinweis auf die Mächtigkeit der Menge der Begründungen. Eine eventuelle Begründung ''mit Rechnen in <math>\mathbb{R}</math>'' ist dabei nicht berücksichtigt. | ||
| + | ====Wie tief gehen die Begründungen==== | ||
| + | Bei Aufgaben, die die Kongruenzgeometrie voraussetzen, braucht nicht mehr mit den Inzidenzaxiomen begründet werden. Wir gehen davon aus, dass jede Gerade unendlich viele Punte hat. | ||
| + | ====Fehler in der Lösung von Übungsaufgabe 11.08 im Tutorium vom Freitag, den 12.07.==== | ||
| + | Im Tutorium am Freitag (12.07.2013) wurde die Lösung von Übungsaufgabe 11.08 nicht korrekt angegeben. Mehr dazu hier:<br /> | ||
| + | [[Die korrekte Lösung von Übungsaufgabe 11.08 und der Fehler im Tutorium]] | ||
| + | |||
| + | ====Sätze am Kreis sind für die Klausur relevant==== | ||
| + | Es ist zwar von der Zeit her eng, aber da sie klassischer Schulstoff sind, bleiben sie als Stoff für die Klausur relevant:<br /> | ||
| + | '''Die Sätze am Kreis'''. Ich werde es heute nicht mehr schaffen, die entsprechenden Dateien in laufende Wiki einzubinden. Aus diesem Grunde hier die Dateien aus dem letzten Sommersemester: | ||
| + | *[[Der Satz des Thales (SoSe 11)]] (ohne Umkehrungen, als Übung sind sie trotzdem nicht schlecht) | ||
| + | *[[Sehnenvierecke und der Satz über die gegenüberliegenden Winkel im Sehnenviereck (SoSe 11)]] | ||
| + | *[[Peripheriewinkelsatz und Zentriwinkel-Peripheriewinkelsatz (SoSe 11)]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | [[Category:Einführung_S]] | ||
| + | [[Category:Didaktik Geometrie]] | ||
Aktuelle Version vom 14. Juli 2013, 16:02 Uhr
Der Berg wurde schon mal bezwungenWas passierte auf dem Königsstuhl?Tips zur Vorbereitung auf die KlausurInhaltlichFaltkonstruktion eines ParallelogrammsEs sei Beweisen wie die SchülerDie Anzahl der Punkte, die es für jeden Schritt des Beweises gibt, ist gleichzeitig ein Hinweis auf die Mächtigkeit der Menge der Begründungen. Eine eventuelle Begründung mit Rechnen in Wie tief gehen die BegründungenBei Aufgaben, die die Kongruenzgeometrie voraussetzen, braucht nicht mehr mit den Inzidenzaxiomen begründet werden. Wir gehen davon aus, dass jede Gerade unendlich viele Punte hat. Fehler in der Lösung von Übungsaufgabe 11.08 im Tutorium vom Freitag, den 12.07.Im Tutorium am Freitag (12.07.2013) wurde die Lösung von Übungsaufgabe 11.08 nicht korrekt angegeben. Mehr dazu hier: Sätze am Kreis sind für die Klausur relevantEs ist zwar von der Zeit her eng, aber da sie klassischer Schulstoff sind, bleiben sie als Stoff für die Klausur relevant:
|




 geschafft
geschafft 



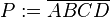 ein weißes Blatt Papier im Format DIN A4. Wie faltet man mit
ein weißes Blatt Papier im Format DIN A4. Wie faltet man mit  ein Parallelogramm, wenn man die Seiten
ein Parallelogramm, wenn man die Seiten 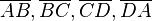 in keiner Art und Weise für die Faltkonstruktion verwenden darf?
in keiner Art und Weise für die Faltkonstruktion verwenden darf?
 ist dabei nicht berücksichtigt.
ist dabei nicht berücksichtigt.

