Lösung von Aufgabe 10.4P (SoSe 13): Unterschied zwischen den Versionen
(table+) |
(→Beweis von Nolessonlearnd) |
||
| Zeile 77: | Zeile 77: | ||
| 3); (4); (5) | | 3); (4); (5) | ||
|}--[[Benutzer:Nolessonlearned|Nolessonlearned]] 19:35, 17. Jul. 2013 (CEST)<br /> | |}--[[Benutzer:Nolessonlearned|Nolessonlearned]] 19:35, 17. Jul. 2013 (CEST)<br /> | ||
| + | Das löst das Problem leider nicht: Du nennst in Schritt 1 einen Punkt Q, damit liegt dieser fest. Erst in Schritt 3 nennst du, dass er zu P und P´´ den gleichen Abstand hat. Hat er aber - wenn nicht zufällig so gezeichnet - gar nicht. Geht echt nicht. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 20:06, 17. Jul. 2013 (CEST) | ||
==Beweis von Wüstenfuchs== | ==Beweis von Wüstenfuchs== | ||
Version vom 17. Juli 2013, 19:06 Uhr
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke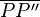 
, mit 
.
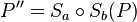Voraussetzung:
a ∩ b = {S} ∧ a ⊥ b --Nolessonlearned 18:24, 13. Jul. 2013 (CEST)
Behauptung:
S ist Mittelpunkt von P͞,P͞``
mit P``= Sa∘Sb(P) --Nolessonlearned 18:24, 13. Jul. 2013 (CEST)
Beweis von Nolessonlearnd
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | ∃m: m ∩ a ∩ b = {S}
mit m ≠ a,b |
Voraussetzung;
Konstruktion der Gerade m |
| 2) | Es existiert Q Element von m: Q͞P kongruent Q͞P͞`` | (1); Mittelsenkrechtenkriterium |
| 3) | m senkrecht P͞P͞`` | (2); Def. Mittelsenkrechte |
| 4) | PS| = |SP'| | (3); Mittelsenkrechtenkriterium |
| 5) | S ist Mittelpunkt von P͞P͞`` | (1); (2); (3); (4); Voraussetzung |
Kreative Beweisidee. Zwei Probleme fallen mir auf:
1. Du kannst nicht erst die GErade m konstruieren (dann ist sie bereits fest) und sie dann später als Mittelsenkrechte deuten. (Schritt 2 und 3) - > Diese Schwierigkeit lässt sich leicht beheben.
2. Du kannst nicht in Schritt 5 sagen, dass S Mittelpunkt von PP´´ ist, da dafür laut Def. Mittelpunkt zwei Dinge erfüllt sein müssen: 1.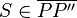 
und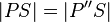 
. Ersteres hast du noch nicht gezeigt. --Tutorin Anne 14:04, 16. Jul. 2013 (CEST)
Neuer Versuch
| Beweisschritt | Begründung | |
|---|---|---|
| 1) |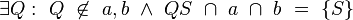 
|
Voraussetzung; Konstruktion der Gerade QS |
| 2) |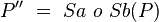 
|
Eigenschaft der Punktspiegelung |
| 3) | Fehler beim Parsen(Lexikalischer Fehler): \left| QP \right| \ =\ \left| QP" \right| | (1); (2); Mittelsenkrechtenkriterium |
| 4) | Fehler beim Parsen(Lexikalischer Fehler): \left\{ {S} \right\}\ =\ QS\ \cap\ \overline{PP"} \ \wedge\ QS\ \perp \ \overline{PP"} | (1); (2); (3); Def. Mittelsenkrechte |
| 5) | Fehler beim Parsen(Lexikalischer Fehler): \left| PP" \right|\ =\ \left| PS \right|\ +\ \left| SP" \right| | Def. Zwischen; Eigenschaft der Mittelsenkrechte |
| 6) | Fehler beim Parsen(Lexikalischer Fehler): S\ ist\ Mittelpunkt\ von\ \overline{PP"} | 3); (4); (5) |
Das löst das Problem leider nicht: Du nennst in Schritt 1 einen Punkt Q, damit liegt dieser fest. Erst in Schritt 3 nennst du, dass er zu P und P´´ den gleichen Abstand hat. Hat er aber - wenn nicht zufällig so gezeichnet - gar nicht. Geht echt nicht. --Tutorin Anne 20:06, 17. Jul. 2013 (CEST)
Beweis von Wüstenfuchs
| Voraussetzung | a⊥b ∧ a∩b = {S} ∧ Sa∘Sb(P)= P`` |
| Behauptung | IPSI = ISP``I (das ist nicht die komplette Behauptung; s.Anmerkung oben.) |
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| 1 | Drehe a⊥b so das P  a und S fest |
Vor. ; |
| 2 | Sa(P) = P' = P | 1.) ; Def. Geradenspiegelung |
| 3 | Sb(P') = P`` mit P`` a |
2.) ; a ist Fixgerade bezüglich der 
|
| 4 | IPSI = ISP``I | 3.) ; Def. Geradenspiegelung |
| 4b | |
... |
| 5 | |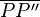
4.)+4b) ; Def. Mittelpunkt |
--Wüstenfuchs 20:42, 15. Jul. 2013 (CEST)
Der Beweis ist fast korrekt. Auch hier fehlt die Begründung, dass S auch Element der Strecke PP´´ ist, weil er nur dann Mittelpunkt von PP`` ist. Optimalerweise dafür noch ein Extraschritt einbauen, oder aber die Begründung in 5) ergänzen. --Tutorin Anne 14:13, 16. Jul. 2013 (CEST)
