Lösung von Zusatzaufgabe 6.1P (SoSe 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>.<br /><br /> | Beweisen Sie: Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>.<br /><br /> | ||
| − | '''Voraussetzung''':<math>Zw(A,B,C)\ mit\ A,B,C\ \in\ E</math> <br /><br /> | + | '''Voraussetzung''': <math>Zw(A,B,C)\ mit\ A,B,C\ \in\ E</math> <br /><br /> |
| − | '''Behauptung''':<math>koll(A,B,C)</math><br /><br /> | + | '''Behauptung''': <math>koll(A,B,C)</math><br /><br /> |
| Zeile 13: | Zeile 13: | ||
| <math>\left| AC \right| =\left| AB \right| +\left| BC \right|</math> | | <math>\left| AC \right| =\left| AB \right| +\left| BC \right|</math> | ||
| Voraussetzung; Def. Zwischen | | Voraussetzung; Def. Zwischen | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| 5) | | 5) | ||
| <math>koll(A,B,C)</math> | | <math>koll(A,B,C)</math> | ||
| − | | (1); | + | | (1); Dreiecksungleichung |
q.e.d. | q.e.d. | ||
|}<br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 21:30, 18. Jul. 2013 (CEST) | |}<br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 21:30, 18. Jul. 2013 (CEST) | ||
| − | + | Schritt 1 ist korrekt. Alle weiteren Zwischenschritte sind Quatsch. In Satz "Dreiecksungleichung" steht direkt drin, dass daraus kollinear folgt. Der Beweis hat also nur 2 Schritte. Schau dir nochmal gut die Dreiecksungleichung an - da steckt ne Menge Begründungspotenzial!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:51, 19. Jul. 2013 (CEST) | |
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 19. Juli 2013, 11:19 Uhr
Beweisen Sie: Aus  folgt
folgt  .
.
Voraussetzung: 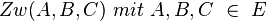
Behauptung: 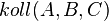
| Beweisschritt | Begründung | |
|---|---|---|
| 1) | 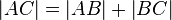
|
Voraussetzung; Def. Zwischen |
| 5) | 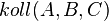
|
(1); Dreiecksungleichung
q.e.d. |
--Nolessonlearned 21:30, 18. Jul. 2013 (CEST)
Schritt 1 ist korrekt. Alle weiteren Zwischenschritte sind Quatsch. In Satz "Dreiecksungleichung" steht direkt drin, dass daraus kollinear folgt. Der Beweis hat also nur 2 Schritte. Schau dir nochmal gut die Dreiecksungleichung an - da steckt ne Menge Begründungspotenzial!--Tutorin Anne 10:51, 19. Jul. 2013 (CEST)

