Lösung von Zusatzaufgabe 6.1P (SoSe 13)

Beweisen Sie: Aus $\operatorname{Zw} \left( A, B, C \right)$ folgt $\operatorname{koll} \left( A, B, C \right)$.

Voraussetzung: 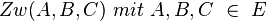$Zw(A,B,C)\ mit\ A,B,C\ \in\ E$

Behauptung: 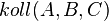$koll(A,B,C)$

	Beweisschritt	Begründung
1)	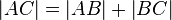$\left| AC \right| =\left| AB \right| +\left| BC \right|$	Voraussetzung; Def. Zwischen
5)	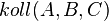$koll(A,B,C)$	(1); Dreiecksungleichung q.e.d.

--Nolessonlearned 21:30, 18. Jul. 2013 (CEST)

Schritt 1 ist korrekt. Alle weiteren Zwischenschritte sind Quatsch. In Satz "Dreiecksungleichung" steht direkt drin, dass daraus kollinear folgt. Der Beweis hat also nur 2 Schritte. Schau dir nochmal gut die Dreiecksungleichung an - da steckt ne Menge Begründungspotenzial!--Tutorin Anne 10:51, 19. Jul. 2013 (CEST)