Übung 2: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Falkonstruktion der Ellipse= ==Aufgabe 1== Es sei <math>p=\frac{1}{2}</math>, <math>F=(0,\frac{p}{2}</math>. Die Gerade <math>l</math> sei durch die Gleichung <…“) |
*m.g.* (Diskussion | Beiträge) (→Reflexion) |
||
| (10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | = | + | =Faltkonstruktion der Parabel= |
| − | + | ==Normalparabel== | |
| − | == | + | Es sei <math>p=\frac{1}{2}</math>, <math>F=\left(0,\frac{p}{2}\right)</math>. <br /> Die Gerade <math>l</math> sei durch die Gleichung <math>y=-\frac{p}{2}</math> gegeben. <br /><math>L=\left(x,-\frac{p}{2}\right)</math> sei ein beliebiger Punkt auf <math>l</math>. <br />Der Punkt <math>P</math> sei der Schnittpunkt der Mittelsenkrechten <math>m</math> von <math>\overline{LF}</math> mit der in <math>L</math> auf <math>l</math> errichteten Senkrechten <math>s</math>. |
| − | Es sei <math>p=\frac{1}{2}</math>, <math>F=(0,\frac{p}{2}</math>. Die Gerade <math>l</math> sei durch die Gleichung <math>y=-\frac{p}{2}</math> gegeben. <math>L=(x,-\frac{p}{2}</math> sei ein beliebiger Punkt auf <math>l</math>. Der Punkt <math>P</math> sei der Schnittpunkt der Mittelsenkrechten <math>m</math> von <math>\overline{LF}</math> mit der in <math>L</math> auf <math>l</math> errichteten Senkrechten <math>s</math>. | + | ===Aufgabe 1=== |
Man beweise: <math>m</math> ist Tangente an die Normalparabel <math>y(x)=x^2</math> in <math>P</math>. | Man beweise: <math>m</math> ist Tangente an die Normalparabel <math>y(x)=x^2</math> in <math>P</math>. | ||
| + | |||
| + | ===Aufgabe 2=== | ||
| + | Man beweise: <math>|FP|=|Pl|</math>. | ||
| + | |||
| + | ===Aufgabe 3=== | ||
| + | Gegeben sei der Punkt <math>K\left(x_k,y_k\right)</math>. Man beweise: | ||
| + | <br /> | ||
| + | <math>y_k=x_k^2 \Rightarrow |FK|=|Kl|</math> | ||
| + | ==Parabel: <math>y(x)=ax^2</math>== | ||
| + | ===Aufgabe 4=== | ||
| + | Die Lösung der Aufgaben 2 und 3 hätte sich nicht zwangsläufig auf die Normalparabel beziehen müssen. Formulieren Sie eine Definition für den Begriff Parabel: | ||
| + | |||
| + | {{Definition|Parabel <br /> Es seien <math> l</math> eine Gerade und <math>F</math> ein Punkt außerhalb von <math>l</math>. Unter der Parabel mit der Leitgeraden <math>l</math> und dem Brennpunkt <math>F</math> versteht man die Menge aller Punkte <math>P</math> mit ... . }} | ||
| + | ===Aufgabe 5=== | ||
| + | Der Brennpunkt <math>F</math> einer Parabel mit der Funktionsgleichung <math>y(x)=ax^2, a \in \mathbb{R}</math> habe zur Leitgeraden <math>l</math> den Abstand <math>p</math>. Man drücke <math>a</math> mittels <math>p</math> aus. | ||
| + | |||
| + | ===Aufgabe 6=== | ||
| + | Gegeben sei die Parabel <math>p</math> durch <math>y(x)=ax^2, a \in \mathbb{R}, a \not= 0</math>. Man beweise: ein zur y-Achse paralleler Lichtstrahl <math>w</math>, der von innen auf <math>p</math> trifft, wird so reflektiert, dass er durch den Brennpunkt <math>F</math> von <math>p</math> geht. | ||
| + | =Experimentierumgebungen:= | ||
| + | ==Normalparabel== | ||
| + | <ggb_applet width="850" height="554" version="4.2" ggbBase64="UEsDBBQACAgIAHWYcEMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAB1mHBDAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1ZW2/buBJ+7v6KgbAPLRDbpG6WCruLpEBwCqQXnHQXB+dhF5RE29zIko4kO3bRH3+GpCjLVnNxnN1NU4ekNBzOfDPzkXQmv2yWKax5WYk8m1p0SCzgWZwnIptPrVU9GwTWL+9+msx5PudRyWCWl0tWTy13aFu7eTga+kROFsnUmvHYZm4YDWaRSweu53oDFgbuwPHcWeyElMaOawFsKvE2yz+xJa8KFvPreMGX7CqPWa10Luq6eDsa3d7eDs3qw7ycj+bzaLipEgvQ8qyaWk3nLarbm3TrKHGbEDr6z8crrX4gsqpmWcwtkF6txLufXk1uRZbkt3ArknoxtYLx2IIFF/MFuumH1IKRFCrQ14LHtVjzCqd2hsrnellYSoxl8v0r3YO0dceCRKxFwsupRYbUs8eh41PXCz2bktC3IC8Fz+pG2Cw6Muoma8FvtV7ZU0u6JERL16ISUcoRdZZW6JbIZiVCihaVKxxW9TblESvNeGcQPcMfFBDfuNSFsdM4TC07JGc2HZ+NCTnzPKJt6S5sQZ3nqdJKwAvh+3ewiU3gTDZUNzY2vq9fEf2MOLqxdePqxtMyrp7ualFXy7haxnXu8bMZ7xxtHux5avx0un5S9E9+fPwoAA78DDp+UunEd6DSetU4IO2myn7ZuM3Q18OxaijRDW1eBvKXwss/0SPnSR7Rzqo6H+5etJcvZsXAO2JF+yQ/Wy+pZIzDNW3vDi9PBLddtOsorqX+q09vSecoP++E9ogVffeU2n/CgmOyV/am5nVLm/Y+GJ7NqMnIsOGkMQiqhZRtUrrmy0qa6ISKnICCh8Xrj5FLPKAhNmNZxDZQD1wPhzQAX7ZjcGTduuBAAFKOOqAoyAvwl6tq2gcPdcmHY13c4LjgOUAVcbmAKIAiP8TEdlDC88DDSXJ1Kpd1fHB9HDgBuGigpL2xpBYH5+EYF7fBoeDIuXQMtg++DWNJndSVjOoH0nZUaoNPwJdTkTuRNzVn4owAHOkNVkGRV6IFd8HToo2KwlFkxarewy5eJqZb5wfSSR7fXBxgzVlVmz4K4Ya12xf1Bra3bb6apCziKR4urmUaAKxZKqtc6Z/lWQ0mBWz9bF6yYiHi6prXNc6q4E+2Zles5ptLlK6MgWpptZtP+CpORSJY9hvmiFQhFUK7ucvUMpu7Z/t6lTjPy+R6W2HiwOa/vMzRptAf+k7g0zAMHIq7IW612+ZVgCcdH3kXldmEepi2MZMJ73p06Dhj4vg+oYEdhlii2zveNf7xdesZ2/DKQDkvRdLtf6gu8jRpw1HkIqvfs6JeleqchjRZSpfOs3nKFbKKePHEE99E+ea6oVCt6+u2wBHR60fz93mal4DlaHvoybxpI90qGWlYK0WUDFESxMRIJO17ip5JCdVGulVSGHRtWuMoNV5SYpYRlSIaVN5NMZUx8vy0ykR9ZQa1iG8aT6mW/7RaRphszbR9lfSZVE5GB+k1ueFlxlOdRBkGcpWvKp3VbWa+mqwq/oXVi/Ms+TefYzl+YZIRa1StRXcWJzwWS5yonzfQMRnWX9FU/TTh85IbD1N1MNbAqrekm9K9x0rVZZkvP2Trr5gzB6ZORsafSRWXopCZCRFS9A3fZV8iKoYEn3TnofMVehFLskEgawmiBWxVL/JSnX2xZOXGDJ/yNZegIk1iQsp6TfkSD75Qq7TMVkteirgNkT5Uo5Er48ewyUoZH8ijP5Fbdnu4nrSDE9/fkbnA0mLB1Fm8yU+2Rau6WCltH/OkWZkaBDFAyk2ki0KnSsG5TrK6qS0oUJ0qzQ60jafS501R8kpenYzJDKl0g9q2MIXXg+INjMA26mTlaHbdx0o/bxX0QNnL9eMwIfdi8nk2q3gNG2S1EBlOUcuPEHM6qVhJcXVD3DbXzG9ybHuH7FAj3d/gpadSFNYCKjv/EknCszYS/H+ZnlLpokUAUxGLulkV6VECrCz5Of354RhcNjF4Tc6gkAF4Y9ZXfPujEDQvWgVPiYEfqCDIJtLNI8PwCKAVwBJpanQpi+WGsDdTP+2TyB6Gl30M98BADuhUbvKPJOTAVX479+J0WMKSAx5XxE9MVDHn2RohyJHwYUNMfIipBNPZUPRA9ba0EfpGO8FDq0uxgXNixM6N2LltOo7puKbjdVjzmJrZvt68mW5+tx9ROtd/UFM8A3rWMtixBSTVPInbn6GGyGENNYHAzklV9BBwtgHuJNzsl4Pb88MW58slyxLI1DXyms/lc2t3gWGkyUBGNRbaz1VtXkZaY6OnB2bVaDRYRQ9QV4cOTueue5A0LG632+UJuyXCkUo2+5DJcydXJ7X+SfWG80JeED5nX0uWVfLb3v0j6t1x+aJScj8qUS8U5/eHYj+vz5+0h1BbX2RU21xknrynPmqvoJ29YmdTh0rI0Cedf9QLn6FEDvn6qkfUjymcc102l71IxccVTfxCimYgq0SfffqYf1Pvqdd9gTf9F1xVV2jUhajU4eEgcnEvZPz+kO1dGPg/cj6zdeKP3cedY+8pHK+NZtCVCJ/xQiGWdx+Olg8UW5sQvaCpcuO92F0cQ4wXf+9No3O+pmMdgEfe+FR8nE4Aiec21Wn2NJ92AxyeTIMfH4jM57Je5PM8Y6msrR+zYX/fmh1RWrOXQoV2ew3UYOOR1t6jPozmX1Itx9cF18DPesC/P6Yu3r+YG/hdzEWGjr+f78+1/X/p5f2o+62c+oa8+Tv6u/8DUEsHCMEmpCD0BwAA9x8AAFBLAQIUABQACAgIAHWYcENFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAdZhwQ8EmpCD0BwAA9x8AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACMCAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | ==Reflexion== | ||
| + | <ggb_applet width="796" height="523" version="4.2" ggbBase64="UEsDBBQACAgIALiYcEMAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAC4mHBDAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbM1aa2/bOBb93PkVhDFYtEDs8CVR6jodpA2KLZA+MOkuFvthF7JE25zIkkaSE7voj99LUrRlK07sxNPGeVCUyEvec+85JG0Pf1vMUnQjy0rl2VmPDHAPySzOE5VNznrzetwPer+9+WU4kflEjsoIjfNyFtVnPT6gvXU/qA18rDur5Kw3ljGNeDjqj0ec9LnHvX4UBrzPPD6OWUhIzHgPoUWlXmf5p2gmqyKK5VU8lbPoMo+j2tic1nXx+vT09vZ24EYf5OXkdDIZDRZV0kMw86w66zUXr8HcRqdbZppTjMnpvz9eWvN9lVV1lMWyh7RXc/XmlxfDW5Ul+S26VUk9PesFlPXQVKrJFNz0ffDpVDcqwNdCxrW6kRV0bVWNz/Ws6JlmUaafv7BXKF2500OJulGJLM96eEB8GpAg9DzMqUcFgxHzUsmsbhqTZtBTZ254o+SttauvzJAchwJioCo1SiWgHqUVuKWycQmQwozKOVSrepnKUVS6+npC5AR+oIH6JrUt8NPicNajIT6hRJwIjE9ginYu7YF7qM7z1FjFyAvR9++IYorRiS6ILSgUvm8fYXsPM1tQW3BbeLYNt925bcptG27bcHaPn0197WhzY8NT5ydr+0nAP/3nw58BYMvPoOUn0U58R0TP3hQM6XkTM39d8Kbq26owBcG2IM3DQP8zePlP9Ig9yiPSGtXmw+5BO/niRhShv/+I9El+rrwkWjG2x6TeDi+fCO5qUK8FLYxlfs1fZ0h2kJ87oT1gRJ8/hfuPGFDgDdo7ztuSNOV9MBxtUsNTp4bDZkKomuq2TUrXclbpKbLQiBMiyAPy+gK0xEMkhEJoElNEPMQ9qJIA+boUiGnecsRQgHQ7wpCRIC+Af9xw2kce2NI3hSU3Yhx5DBEjXBwBCsiIH2BCGbTwPORBJz060cMyH3EfKixAHCaoZU9oaWHQD+owOEWMIKb7EoGoj3yKhJZOwrWi+oGeOxilyMfI111BO0E3rWZCjwAx7Q2woMgrtQJ3KtNiFRWDo8qKeb2BXTxL3GWdb7VO8vj67RbWMqpqdw2NYMFar4t2AdtYNl8M02gkU9hcXOk0QOgmSjXLjf1xntXIpQC19yZlVExVXF3JuoZeFfojuokuo1ou3kPryk3QDG1W86Gcx6lKVJT9C3JEm9AGkVvcjXa5xZ2Hnh0lzvMyuVpWkDho8R9Z5jCnMBxQWABpAAKLKQ9BipbNI+ENKAt8HFASBqDuHiRuHOmUZwEdMIZDHwtPCC5gBVnueCTs0PJm5Vq0kJXDclKqpH39oXqbp8kqHkWusvpdVNTz0mzUYHKl9uk8m6TSQGuUF7Y88fUoX1w1GmptfV0WUMN2/NHkXZ7mJQI+Ug8cmTTlyJamjZ7YqhU2bbBpgV2QVLJ6TkJqWphyZEvTCqJup9Y4SpyXBLthVGWUBoy3c8ykjN5AzTNVX7pKreLrxlNi23+az0aQbU23TZPkSCaHp1v5NbyWZSZTm0UZBHKezyub1qvUfDGcV/JLVE/Ps+R3OQE+fom0JNZg2jZdzziRsZpBR3u/gS7SYf0nTNXeTeSklM7D1OyMLbDmKW7ndOe2MfW+zGcfspuvkDNbUx2eOn+GVVyqQmcmGoFGX8t19iWqikDhk3Y/cL4CL2KtNgBkrUHsoWheT/PSbH6Bs3plRp/yG6lBBZ2EhNSETeUMdr6oNmmZzWeyVPEqRHZXDZOcOz8GTVbq+KB89AeIy3oRt53WcMLzHZmLorSYRmYz3uRntIRZtbEy1j7mSTMycQhCgIyboBeFTZVCSptkdcMtVIA5Q80WtI2n2udFUcpKn53clCPQ0gVYW6Iz9LJfvEKniDpzmjlWXjexsvdXBjqgbOT6YZjgezH5PB5XskYLLaGgcEZa7kKMtVKx0s3NEXHZnDO/6Tr1ttWhBr2/hlNPZSRsBai++IdKEpmtIiH/zGyXypIWAExVrOpmVJBHDbCZya/prw/H4H0Tg5f4BBU6AK/c+EZv7wpB82Bl4DEx8AMTBF2MbLFnGPYA2gCskSbOlpmxXhA2etq7XRHZwPB9F8MNMEADWsxNfkpC9rnxm92L0zaFtQbsR+JHJqqayOwGIMhB8NECu/hgxwR3sSDggblakqbRN9IKHsy6VAt0jl2zc9fsnLoL5i64u/BaqnkIZ5YvF6/OFv+le1Dn6n/EkadPTlYKdiiBtJlHafsROIS3OdQEAi6exKKHgKMOuCfhRp8PbseHLc5nsyhLUGbOkVdyou/31ieYCDcZGBGLhfVzXruHI2uxsdMBs2osOqxGD0hXSw6erl33IOlUnK6WyyeslgBHqtXsQ6b3ndLs1Lo71WspC31A+Jx9LaOs0m/3bm5Rd8fli0nJzaiMOqE4vz8Um3l9/qg1hFB7kDFlc5B59Jq611pBWmvFek4tKcGDwG+9QkGOQJFtvb7sCPU+xDm3tHnfiVR8GGnihxToR7Gmr2liNz9d0L9Z0EnrvuA0eMa0uoRJvVWV2T1shS7uxEzeH7ONE4P8KRs0ak8Mgu+3kb2HOZ6LJhPe+hWQ8IhHCjXbvT2aPUC3VUZ0omYIJzvBe3uINL79wQt+a4tNhA3Bnoc+iBBnLCC8+fWofhNu6fa3RvswWb98/mQl/PhAaD6X9TSf5FmUanbdLYjdpWt8ALnGz2QL0aerk6AFG3a1grVeIe+8P3ccuhxODGmBH3eAf3cIMd49m0P4Lu3CA+G1852FR9sCfHlK4r/bJUyTAxJ/8kwS320C7gyCRTvgoET2l+21A6DHZMFHVZadFX1sQzDpas/foiKv/n6IAjU9nkc4rMbjMBAiJIwHlDdvBApGOA49zkPPfM7iFnXOKKwULPApLO/Y8/6iRf2w40xXmi4OkaaLx63ZxznPrD4AePDta3L3O18PC5vmFPMYpdjnjASMi7/g+P97tLxbty46wZneH5wSLDnkp4/jyfZnZsc6wDBGOQW6AJjYF1iIzTUcTjBBAGSiAfUJpAVsq+6hh/eTTzB3Kt3FLqW72Efptni1S+p+OLs2T6EigBdhIhQ+pfrjVxNDL+CC+DjEmPEw1N82+4EcWYO7AbranynqGTFFf5MOtk8eBq4InwCs7mRBYaERsIAEfoi58ALHGyxIyLnPKBFAnUD4z4o3p+2PUc13GppvPr75P1BLBwgQI6CkPwkAAKkpAABQSwECFAAUAAgICAC4mHBDRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIALiYcEMQI6CkPwkAAKkpAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA1wkAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | [[Kategorie:Linalg]] | ||
Aktuelle Version vom 16. November 2013, 19:08 Uhr
Inhaltsverzeichnis |
Faltkonstruktion der Parabel
Normalparabel
Es sei 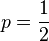 ,
, 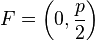 .
.
Die Gerade  sei durch die Gleichung
sei durch die Gleichung 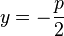 gegeben.
gegeben. 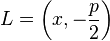 sei ein beliebiger Punkt auf
sei ein beliebiger Punkt auf  .
.
Der Punkt  sei der Schnittpunkt der Mittelsenkrechten
sei der Schnittpunkt der Mittelsenkrechten  von
von 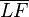 mit der in
mit der in  auf
auf  errichteten Senkrechten
errichteten Senkrechten  .
.
Aufgabe 1
Man beweise:  ist Tangente an die Normalparabel
ist Tangente an die Normalparabel 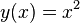 in
in  .
.
Aufgabe 2
Man beweise: 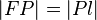 .
.
Aufgabe 3
Gegeben sei der Punkt 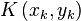 . Man beweise:
. Man beweise:
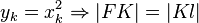
Parabel: 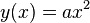
Aufgabe 4
Die Lösung der Aufgaben 2 und 3 hätte sich nicht zwangsläufig auf die Normalparabel beziehen müssen. Formulieren Sie eine Definition für den Begriff Parabel:
Definition
Parabel
Es seien  eine Gerade und
eine Gerade und  ein Punkt außerhalb von
ein Punkt außerhalb von  . Unter der Parabel mit der Leitgeraden
. Unter der Parabel mit der Leitgeraden  und dem Brennpunkt
und dem Brennpunkt  versteht man die Menge aller Punkte
versteht man die Menge aller Punkte  mit ... .
mit ... .
Aufgabe 5
Der Brennpunkt  einer Parabel mit der Funktionsgleichung
einer Parabel mit der Funktionsgleichung 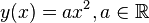 habe zur Leitgeraden
habe zur Leitgeraden  den Abstand
den Abstand  . Man drücke
. Man drücke  mittels
mittels  aus.
aus.
Aufgabe 6
Gegeben sei die Parabel  durch
durch 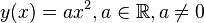 . Man beweise: ein zur y-Achse paralleler Lichtstrahl
. Man beweise: ein zur y-Achse paralleler Lichtstrahl  , der von innen auf
, der von innen auf  trifft, wird so reflektiert, dass er durch den Brennpunkt
trifft, wird so reflektiert, dass er durch den Brennpunkt  von
von  geht.
geht.
Experimentierumgebungen:
Normalparabel
Reflexion

