Der Basiswinkelsatz: Unterschied zwischen den Versionen

Version vom 1. Juli 2010, 22:14 Uhr

Der Basiswinkelsatz

Gleichschenklige Dreiecke

Definition VII.4 : (gleichschenkliges Dreieck)

Das können sie selbst. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.

Übung 11 Aufgabe 1

Der Basiswinkelsatz

Satz VII.5: Basiswinkelsatz

In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.

Für die Schule ok. hier jedoch nicht zugelassen

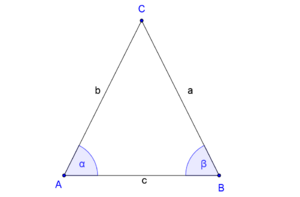
Es sei ein Dreieck mit den schulüblichen Bezeichnungen. o.B.d.A. seien die Seiten und kongruent zueinander:

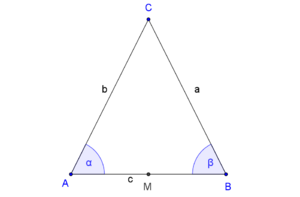
Nach der Existenz und Eindeutigkeit des Mittelpunktes einer Strecke existiert der Mittelpunkt der Dreiecksseite .

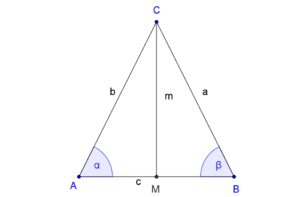
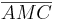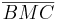Wir werden jetzt zeigen, dass die beiden Teildreiecke und kongruent zueinander sind:

Nachweis von :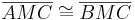

Nr.	Skizze	Beweisschritt	Begründung
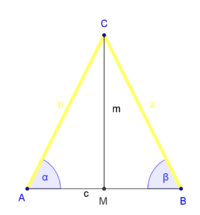
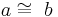
(1)			Voraussetzung
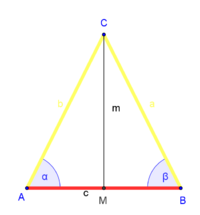
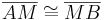
(2)			ist Mittelpunkt von
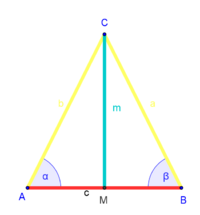
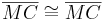
(3)			trivial (oder Reflexivität der Kongruenzrelation)
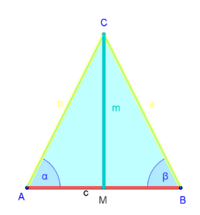
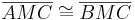
(4)			(1), (2), (3), SSS

Wegen (4) gilt nun auch .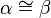

w.z.b.w.

Ein schöner einfacher Beweis, leider hat er hier keine Gültigkeit. Warum?

Ein im Rahmen unserer Theorie korrekter Beweis des Basiswinkelsatzes

Probieren Sie ruhig weitere Varianten: Mittelsenkrechte ... . Letztlich hilft nur die Winkelhalbierende. Damit wir uns auf die wesentliche Beweisidee des Basiwinkelsatzes konzentrieren können, schicken wir ein Lemma voraus.

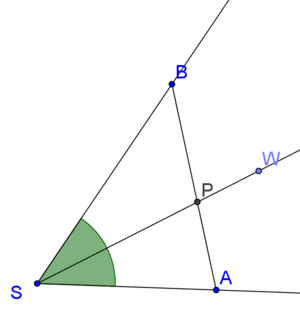
Lemma 1

Die Winkelhalbierende eines Winkels schneidet die Strecke .