Lösung von Zusatzaufgabe 2.5P (WS 13 14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
<br /> | <br /> | ||
Def. 1 ist ungenügend, weil die Eingrenzung auf die Ebene fehlt.<br/> | Def. 1 ist ungenügend, weil die Eingrenzung auf die Ebene fehlt.<br/> | ||
| + | * Das sehe ich anders. Die Eingrenzung auf die Ebene ist in unserem Fall unwesentlich, da wir uns hier sowieso nur auf die Geometrie der Ebene beschränken. Entscheidend finde ich, dass der Begriff der Menge P nicht sicherstellt, dass er alle Punkte des Kreises enthält. Die Menge P könnte z. B. Nur einen Punkt enthalten. Das gibt aber noch keinen Kreis.--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 14:12, 5. Jan. 2014 (CET) <<<br/> | ||
| + | **Dein genannter Punkt trifft ebenfalls zu und begründet so auch, dass die Definition nicht korrekt ist. Bei der Aufgabe wird aber nicht explizit genannt, dass wir uns auf die Ebene beziehen, weshalb auch die erst genannte Begründung richtig ist. Es genügt einen der Gründe zu nennen, um zu belegen, dass die Definition nicht stimmt.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 15:44, 6. Jan. 2014 (CET) | ||
Def. 2 ist Def. 1 in Symbolen.<br/> | Def. 2 ist Def. 1 in Symbolen.<br/> | ||
Def. 3 ist ungenügend, da Punkte, die nicht den Kreis bilden nicht ausgeschlossen sind.<br/> | Def. 3 ist ungenügend, da Punkte, die nicht den Kreis bilden nicht ausgeschlossen sind.<br/> | ||
Aktuelle Version vom 6. Januar 2014, 15:44 Uhr
Welche Definition für Kreis ist richtig? Warum (nicht)?
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Wenn gilt:
eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
- Sei
 ein Punkt und
ein Punkt und  eine Punktmenge. Wenn gilt:
eine Punktmenge. Wenn gilt: 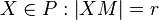 , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  alle Punkte
alle Punkte 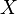 enthält für die gilt∶
enthält für die gilt∶  und
und 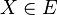 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  genau alle Punkte
genau alle Punkte 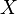 enthält für die gilt∶
enthält für die gilt∶  und
und 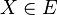 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Menge, deren Elemente Punkte sind. Wenn für alle
eine Menge, deren Elemente Punkte sind. Wenn für alle 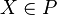 gilt∶
gilt∶  , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Alle Elemente von
eine Menge, deren Elemente Punkte sind. Alle Elemente von  liegen in ein und derselben Ebene wie
liegen in ein und derselben Ebene wie  . Wenn gilt:
. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
Def. 1 ist ungenügend, weil die Eingrenzung auf die Ebene fehlt.
- Das sehe ich anders. Die Eingrenzung auf die Ebene ist in unserem Fall unwesentlich, da wir uns hier sowieso nur auf die Geometrie der Ebene beschränken. Entscheidend finde ich, dass der Begriff der Menge P nicht sicherstellt, dass er alle Punkte des Kreises enthält. Die Menge P könnte z. B. Nur einen Punkt enthalten. Das gibt aber noch keinen Kreis.--EarlHickey (Diskussion) 14:12, 5. Jan. 2014 (CET) <<
- Dein genannter Punkt trifft ebenfalls zu und begründet so auch, dass die Definition nicht korrekt ist. Bei der Aufgabe wird aber nicht explizit genannt, dass wir uns auf die Ebene beziehen, weshalb auch die erst genannte Begründung richtig ist. Es genügt einen der Gründe zu nennen, um zu belegen, dass die Definition nicht stimmt.--Tutorin Anne (Diskussion) 15:44, 6. Jan. 2014 (CET)
Def. 2 ist Def. 1 in Symbolen.
Def. 3 ist ungenügend, da Punkte, die nicht den Kreis bilden nicht ausgeschlossen sind.
Def. 4 ist richtig, da die Problematik aus Def. 3 mithilfe des "genau alle Punkte" beseitigt wurde.
Def. 5 ist ungenügend, da die Punktmenge P nicht alle Punkte des Kreises enthalten muss.
Def. 6 ist fehlerhaft, da man keinen Abstand zwischen einem Punkt und einer Punktmenge setzen kann.
--Knöbelspieß 11:03, 9. Nov. 2013 (CET)
Top!--Tutorin Anne 23:20, 10. Nov. 2013 (CET)

