Lösung von Aufgabe 4.1 P (SoSe 14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> | <math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> | ||
| − | Inwiefern hilft Ihnen diese Äquivalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br /> | + | {| class="wikitable" |
| + | |- | ||
| + | ! A!! B!! A==>B!! ¬B!! ¬A !! ¬B ==> ¬A | ||
| + | |- | ||
| + | | 0|| 0|| '''1'''|| 1|| 1|| '''1''' | ||
| + | |- | ||
| + | | 0|| 1|| '''1'''|| 0|| 1|| '''1''' | ||
| + | |- | ||
| + | | 1|| 0 || '''0'''|| 1|| 0|| '''0''' | ||
| + | |- | ||
| + | | 1|| 1|| '''1'''|| 0|| 0|| '''1''' | ||
| + | |} --[[Benutzer:The Niggster|The Niggster]] ([[Benutzer Diskussion:The Niggster|Diskussion]]) 17:41, 21. Mai 2014 (CEST) | ||
| + | |||
| + | Inwiefern hilft Ihnen diese Äquivalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br /><br /> | ||
| + | |||
Hierbei sieht man, dass die Kontraposition <math>(\neg B \Rightarrow \neg A)</math> äuvivalent zum Satz <math>(\ A \Rightarrow B)</math> ist. Wenn ich also die Kontraposition bewiesen habe, habe ich auch gleich den Satz bewiesen. | Hierbei sieht man, dass die Kontraposition <math>(\neg B \Rightarrow \neg A)</math> äuvivalent zum Satz <math>(\ A \Rightarrow B)</math> ist. Wenn ich also die Kontraposition bewiesen habe, habe ich auch gleich den Satz bewiesen. | ||
| − | --[[Benutzer:Audrey Hepburn|Audrey Hepburn]] ([[Benutzer Diskussion:Audrey Hepburn|Diskussion]]) 12:03, 20. Mai 2014 (CEST) | + | --[[Benutzer:Audrey Hepburn|Audrey Hepburn]] ([[Benutzer Diskussion:Audrey Hepburn|Diskussion]]) 12:03, 20. Mai 2014 (CEST) So ist es.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 19:07, 20. Mai 2014 (CEST) |
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 21. Mai 2014, 17:42 Uhr
Beweisen Sie mit Hilfe einer Wahrheitstabelle:
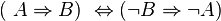
| A | B | A==>B | ¬B | ¬A | ¬B ==> ¬A |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
Inwiefern hilft Ihnen diese Äquivalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Hierbei sieht man, dass die Kontraposition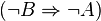 
äuvivalent zum Satz 
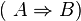ist. Wenn ich also die Kontraposition bewiesen habe, habe ich auch gleich den Satz bewiesen.
--Audrey Hepburn (Diskussion) 12:03, 20. Mai 2014 (CEST) So ist es.--Tutorin Anne (Diskussion) 19:07, 20. Mai 2014 (CEST)
