Lösung von Aufg. 6.4P (SoSe 14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 2: | Zeile 2: | ||
b) Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 6.3 nicht wahr ist. | b) Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 6.3 nicht wahr ist. | ||
| − | a) Kontraposition: Wenn der Durchschnitt zweier Punktmengen nicht konvex ist, dann sind entweder beide Mengen nicht konvex, oder nur eine davon. | + | a) Kontraposition: Wenn der Durchschnitt zweier Punktmengen nicht konvex ist, dann sind entweder beide Mengen nicht konvex, oder nur eine davon.<br /> |
| + | |||
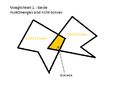
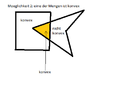
b) Umkehrung: Wenn der Durchschnitt zweier Punktmengen konvex ist, dann sind die zwei Punktmengen auch konvex. | b) Umkehrung: Wenn der Durchschnitt zweier Punktmengen konvex ist, dann sind die zwei Punktmengen auch konvex. | ||
| − | + | <gallery> | |
| + | Datei:Nicht_konvex_1.png| | ||
| + | Datei:Nicht_konvex_2.png| | ||
| + | </gallery> | ||
| + | --[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 15:14, 12. Jun. 2014 (CEST) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Version vom 12. Juni 2014, 14:14 Uhr
a) Formulieren Sie die Kontraposition der Implikation aus Aufgabe 6.3.
b) Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 6.3 nicht wahr ist.
a) Kontraposition: Wenn der Durchschnitt zweier Punktmengen nicht konvex ist, dann sind entweder beide Mengen nicht konvex, oder nur eine davon.
b) Umkehrung: Wenn der Durchschnitt zweier Punktmengen konvex ist, dann sind die zwei Punktmengen auch konvex.
--Picksel (Diskussion) 15:14, 12. Jun. 2014 (CEST)