Lösung von Aufgabe 10.5: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
TimoRR (Diskussion | Beiträge) (→Beweis Versuch 1:) |
|||
| Zeile 39: | Zeile 39: | ||
qed --[[Benutzer:Löwenzahn|Löwenzahn]] 17:51, 1. Jul. 2010 (UTC) | qed --[[Benutzer:Löwenzahn|Löwenzahn]] 17:51, 1. Jul. 2010 (UTC) | ||
| + | |||
| + | Das war ja jetzt der Beweis für die Existenz, fehlt jetzt noch einer für die Eindeutigkeit!? | ||
| + | Wenn ja, wie sähe der dann aus!? Reicht dafür das Winkelkonstruktionsaxiom!? --[[Benutzer:TimoRR|TimoRR]] 17:00, 6. Jul. 2010 (UTC) | ||
Version vom 6. Juli 2010, 18:00 Uhr
Satz VI.1/2:
Es sei 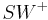 eine Winkelhalbierende des Winkels
eine Winkelhalbierende des Winkels  .
.
Dann gilt: 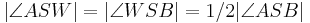
Beweis Versuch 1:
VSS: 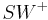 eine Winkelhalbierende des Winkels
eine Winkelhalbierende des Winkels 
Beh: 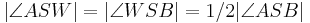
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 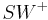 eine Winkelhalbierende von eine Winkelhalbierende von 
|
(VSS) |
| (II) | 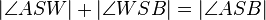
|
Winkeladditionsaxiom, W liegt im Innern von 
|
| (III) | 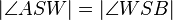
|
(I), Def. Winkelhalbierende |
| (IV) | 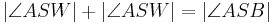
|
(II), (III), (rechnen mit reellen Zahlen) |
| (V) | 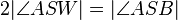 --> --> 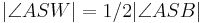
|
(IV), (rechnen mit reellen Zahlen) |
| (VI) | 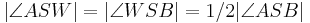
|
(III), (V) |
qed --Löwenzahn 17:51, 1. Jul. 2010 (UTC)
Das war ja jetzt der Beweis für die Existenz, fehlt jetzt noch einer für die Eindeutigkeit!? Wenn ja, wie sähe der dann aus!? Reicht dafür das Winkelkonstruktionsaxiom!? --TimoRR 17:00, 6. Jul. 2010 (UTC)

