Lösung von Zusatzaufgabe 2.5P (SoSe 16): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Welche Definition für Kreis ist richtig? Warum (nicht)?<br /> * Sei <math>M</math> ein Punkt und <math>P</math> eine Menge, deren Elemente Punkte sind. Wenn …“) |
Lili S (Diskussion | Beiträge) |
||
| Zeile 9: | Zeile 9: | ||
| − | + | Definitionen eins und zwei sind keine Definitionen für einen Kreis, da diese nicht beschreiben, wo die Punkte liegen. Die Menge aller Punkte P und der Punkt M können in unterschiedlichen Ebenen liegen. | |
| + | Definition drei ist meiner Meinung nach eine korrekte Definition. <br /> | ||
| + | --[[Benutzer:Lili S|Lili S]] ([[Benutzer Diskussion:Lili S|Diskussion]]) 13:01, 3. Mai 2016 (CEST) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Version vom 3. Mai 2016, 12:01 Uhr
Welche Definition für Kreis ist richtig? Warum (nicht)?
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Wenn gilt:
eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
- Sei
 ein Punkt und
ein Punkt und  eine Punktmenge. Wenn gilt:
eine Punktmenge. Wenn gilt: 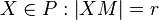 , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  alle Punkte
alle Punkte 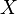 enthält für die gilt∶
enthält für die gilt∶  und
und 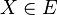 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  genau alle Punkte
genau alle Punkte 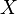 enthält für die gilt∶
enthält für die gilt∶  und
und 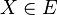 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Menge, deren Elemente Punkte sind. Wenn für alle
eine Menge, deren Elemente Punkte sind. Wenn für alle 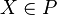 gilt∶
gilt∶  , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Alle Elemente von
eine Menge, deren Elemente Punkte sind. Alle Elemente von  liegen in ein und derselben Ebene wie
liegen in ein und derselben Ebene wie  . Wenn gilt:
. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
Definitionen eins und zwei sind keine Definitionen für einen Kreis, da diese nicht beschreiben, wo die Punkte liegen. Die Menge aller Punkte P und der Punkt M können in unterschiedlichen Ebenen liegen.
Definition drei ist meiner Meinung nach eine korrekte Definition.
--Lili S (Diskussion) 13:01, 3. Mai 2016 (CEST)

