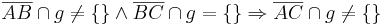Probeklausur: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: == Aufgabe 1 == Die Aufgabe 1 der Probeklausur wurde als Quiz 11 hinterlegt: Quiz_der_Woche_11 == Aufgabe 2 == Definieren Sie den Begriff Strahl <math>\ AB^{+}</ma...) |
(→Aufgabe P5) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == Aufgabe | + | == Aufgabe P1 == |
Die Aufgabe 1 der Probeklausur wurde als Quiz 11 hinterlegt: [[Quiz_der_Woche_11]] | Die Aufgabe 1 der Probeklausur wurde als Quiz 11 hinterlegt: [[Quiz_der_Woche_11]] | ||
| − | == Aufgabe | + | == Aufgabe P2 == |
Definieren Sie den Begriff Strahl <math>\ AB^{+}</math>. Verwenden Sie dabei den Begriff Strecke. | Definieren Sie den Begriff Strahl <math>\ AB^{+}</math>. Verwenden Sie dabei den Begriff Strecke. | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe P2]] |
| − | == Aufgabe | + | == Aufgabe P3 == |
Definition (gemeiner Dreiecksschneider): Unter einem gemeinen Dreiecksschneider versteht man eine Gerade, die alle drei offenen Seiten eines Dreiecks schneidet. <br\> Beschreiben Sie die Menge aller gemeinen Dreiecksschneider und begründen Sie Ihre Aussage. | Definition (gemeiner Dreiecksschneider): Unter einem gemeinen Dreiecksschneider versteht man eine Gerade, die alle drei offenen Seiten eines Dreiecks schneidet. <br\> Beschreiben Sie die Menge aller gemeinen Dreiecksschneider und begründen Sie Ihre Aussage. | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe P3]] |
| − | == Aufgabe | + | == Aufgabe P4 == |
Es seien <math>\ A </math>, <math>\ B </math> und <math>\ C </math> drei paarweise verschiedene Punkte. Beweisen Sie: <math> Zw(A,B,C) \Rightarrow \neg Zw(B,A,C) </math> | Es seien <math>\ A </math>, <math>\ B </math> und <math>\ C </math> drei paarweise verschiedene Punkte. Beweisen Sie: <math> Zw(A,B,C) \Rightarrow \neg Zw(B,A,C) </math> | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe P4]] |
| − | == Aufgabe | + | == Aufgabe P5 == |
| − | Gegeben seien drei paarweise verschiedene und kollineare Punkte <math>\ A </math>, <math>\ B </math> und <math>\ C </math> in einer Ebene <math>\ E </math>. Ferner sei eine Gerade <math>\ g </math> Teilmenge der Ebene <math>\ E </math>, wobei keiner der Punkte <math>\ A </math>, <math>\ B </math> und <math>\ C </math> auf <math>\ g </math> liegen möge. Beweisen Sie | + | Gegeben seien drei paarweise verschiedene und kollineare Punkte <math>\ A </math>, <math>\ B </math> und <math>\ C </math> in einer Ebene <math>\ E </math>. Ferner sei eine Gerade <math>\ g </math> Teilmenge der Ebene <math>\ E </math>, wobei keiner der Punkte <math>\ A </math>, <math>\ B </math> und <math>\ C </math> auf <math>\ g </math> liegen möge. Beweisen Sie folgenden Zusammenhang: <br\> |
<math>\overline {AB} \cap g \neq \lbrace \rbrace \and \overline {BC} \cap g = \lbrace \rbrace \Rightarrow \overline {AC} \cap g \neq \lbrace \rbrace </math> | <math>\overline {AB} \cap g \neq \lbrace \rbrace \and \overline {BC} \cap g = \lbrace \rbrace \Rightarrow \overline {AC} \cap g \neq \lbrace \rbrace </math> | ||
| − | [[Lösung von Aufgabe | + | [[Lösung von Aufgabe P5]] |
Aktuelle Version vom 8. Juli 2010, 12:24 Uhr
Inhaltsverzeichnis[Verbergen] |
Aufgabe P1
Die Aufgabe 1 der Probeklausur wurde als Quiz 11 hinterlegt: Quiz_der_Woche_11
Aufgabe P2
Definieren Sie den Begriff Strahl 
. Verwenden Sie dabei den Begriff Strecke.
Lösung von Aufgabe P2
Aufgabe P3
Definition (gemeiner Dreiecksschneider): Unter einem gemeinen Dreiecksschneider versteht man eine Gerade, die alle drei offenen Seiten eines Dreiecks schneidet.
Beschreiben Sie die Menge aller gemeinen Dreiecksschneider und begründen Sie Ihre Aussage.
Lösung von Aufgabe P3
Aufgabe P4
Es seien 
, 
und 
drei paarweise verschiedene Punkte. Beweisen Sie: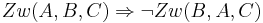 
Aufgabe P5
Gegeben seien drei paarweise verschiedene und kollineare Punkte , und in einer Ebene 
. Ferner sei eine Gerade 
Teilmenge der Ebene , wobei keiner der Punkte , und auf liegen möge. Beweisen Sie folgenden Zusammenhang:
