Was ist eine Gruppe? SoSe 2017: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Das Linkseinslement ist auch Rechtseinslement) |
*m.g.* (Diskussion | Beiträge) (→Das Linkseinslement ist auch Rechtseinslement) |
||
| Zeile 31: | Zeile 31: | ||
Die lange Version der Gruppendefinition fordert, dass wenn das Einselement <math>e</math> sowohl rechtsseitig als auch linksseitig multipliziert mit einem beliebigen Gruppenelement <math>a</math> multipliziert eben dieses Element <math>a</math> das Ergebnis dieser Multiplikation ist. Die kurze Version der Gruppendefinition fordert nur die Existenz eines linksseitigen Einslementes. In der Tat ist die Korrektheit der Gruppendefinition gewährleistet, wenn die Existenz des Einselementes nur linksseitig (oder rechtsseitig) gefordert wird. | Die lange Version der Gruppendefinition fordert, dass wenn das Einselement <math>e</math> sowohl rechtsseitig als auch linksseitig multipliziert mit einem beliebigen Gruppenelement <math>a</math> multipliziert eben dieses Element <math>a</math> das Ergebnis dieser Multiplikation ist. Die kurze Version der Gruppendefinition fordert nur die Existenz eines linksseitigen Einslementes. In der Tat ist die Korrektheit der Gruppendefinition gewährleistet, wenn die Existenz des Einselementes nur linksseitig (oder rechtsseitig) gefordert wird. | ||
Gleiches gilt für die Forderung nach der Existenz linksseitiger bzw. rechtsseitiger inverser Elemente. <br /> | Gleiches gilt für die Forderung nach der Existenz linksseitiger bzw. rechtsseitiger inverser Elemente. <br /> | ||
| − | Es gilt der Satz: | + | Es gilt der Satz:<br /> |
| − | + | ||
| + | =====Satz 1===== | ||
| + | :Wenn in einer Halbgruppe ein linksseitiges Einselement und zu jedem Element der Halbgruppe ein linksseitiges inverses Element existiert, so sind dieses Linkseinselement und diese Linksinversen gleichzeitig Rechtseinselement und Rechtsinverse.<br /> | ||
| + | |||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Version vom 1. Mai 2017, 13:04 Uhr
Beispiele für Gruppenendliche GruppenDie Gruppe der Deckabbildungen des RechtecksDie Gruppe der Deckabbildungen der Rauteunendliche Gruppen Gebrochene Zahlen:
|
![[\mathbb{Q}^+, \cdot ]](/images/math/2/9/8/298e82ce4345a135cfc73e8ba6154d2b.png)
![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png)
 eine nichtleere Menge auf der eine Verknüpfung
eine nichtleere Menge auf der eine Verknüpfung  .
. ![\mathbb{G}:=[G, \odot ]](/images/math/b/6/2/b62276da8758fad83c54ead688c9ecca.png) Gruppe:
Gruppe: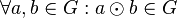
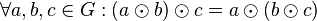
 :
: 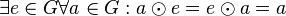 .
.
 aus
aus 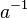 :
: 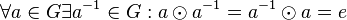 .
.
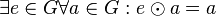 .
.
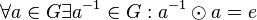 .
.

