Lösung von Aufgabe 2.05 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
(→Lösung 1) |
||
| Zeile 5: | Zeile 5: | ||
Formulieren Sie eine Konstruktionsvorschrift für <math>M_s</math>. | Formulieren Sie eine Konstruktionsvorschrift für <math>M_s</math>. | ||
==Lösung 1== | ==Lösung 1== | ||
| + | Man zeichnet eine Strecke <math>\overline{AB}</math>. Den Zirkel sticht man in Punkt <math>A</math> ein, wählt den Radius so, dass er größer ist als die Strecke <math>\overline{AM}</math> (<math>M</math> ist der Mittelpunkt der Strecke <math>\overline{AB}</math>) und zieht einen Halbkreis in Richtung des Punktes <math>B</math>. | ||
| + | Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt <math>B</math> ein. | ||
| + | Somit ergeben sich zwei Schnittpunkte (oberhalb und unterhalb der Strecke <math>\overline{AB}</math>), die man zur sogenannten "Mittelsenkrechten" <math>M_s</math> verbindet. Für alle Punkte <math>P</math>, die auf <math>M_s</math> liegen, gilt <math>|AP|=|PB|</math>. | ||
| + | |||
==Lösung 2== | ==Lösung 2== | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Version vom 5. Mai 2017, 15:28 Uhr
|
Gegeben sei die Strecke Lösung 1Man zeichnet eine Strecke Lösung 2 |
 . Wir betrachten jetzt die folgende Menge
. Wir betrachten jetzt die folgende Menge 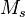 von Punkten
von Punkten  :
: 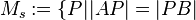 .
. ein, wählt den Radius so, dass er größer ist als die Strecke
ein, wählt den Radius so, dass er größer ist als die Strecke 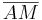 (
( ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke  .
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt
.
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt 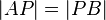 .
.

