|
Gegeben sei die Strecke  . Wir betrachten jetzt die folgende Menge . Wir betrachten jetzt die folgende Menge 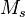 von Punkten von Punkten  : : 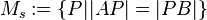 . .
Formulieren Sie eine Konstruktionsvorschrift für 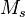 . .
Lösung 1
Lösung von Maaurtoc
Man zeichnet eine Strecke  . Den Zirkel sticht man in Punkt . Den Zirkel sticht man in Punkt  ein, wählt den Radius so, dass er größer ist als die Strecke ein, wählt den Radius so, dass er größer ist als die Strecke 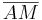 ( ( ist der Mittelpunkt der Strecke ist der Mittelpunkt der Strecke  ) und zieht einen Halbkreis in Richtung des Punktes ) und zieht einen Halbkreis in Richtung des Punktes  .
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt .
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt  ein.
Somit ergeben sich zwei Schnittpunkte (oberhalb und unterhalb der Strecke ein.
Somit ergeben sich zwei Schnittpunkte (oberhalb und unterhalb der Strecke  ), die man zur sogenannten "Mittelsenkrechten" ), die man zur sogenannten "Mittelsenkrechten" 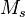 verbindet. Für alle Punkte verbindet. Für alle Punkte  , die auf , die auf 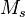 liegen, gilt liegen, gilt 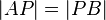 . .
Kommentar --*m.g.* (Diskussion) 12:28, 7. Mai 2017 (CEST)
Passt, wobei der Radius der Kreisbögen nur größer als die Hälfte der Länge der Strecke sein muss, was nicht an der Korrektheit Ihrer Vorschrift rüttelt.
Bezüglich der Eleganz der Formulierungen ist noch ein wenig Luft, aber das wird.
Als ich in der 6. Klasse war und derartiges formulieren musste, rügte der Lehrer sofort bei der Formulierung "Wir stechen mit dem Zirkel ...": "WIR STECHEN, SCHLAGEN, HAUEN NICHT!". Als Lehrer fand ich dann einen schönen Rechtschreibfehler in der Konstruktionsbeschreibung eines Schülers: "Wir schlagen einen GREIS ..."
Eleganter wäre:
- Zeichne um
 einen Kreis einen Kreis 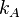 mit einem Radius mit einem Radius  , der größer als die Hälfte der Länge von , der größer als die Hälfte der Länge von  ist. ist.
- Zeichne um
 einen Kreis einen Kreis 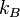 mit demselben Radius mit demselben Radius  . .
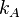 und und 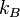 schneiden sich in den zwei Punkten schneiden sich in den zwei Punkten  und und 
- Zeichne die Gerade
 , sie ist die gesuchte Punktmenge. , sie ist die gesuchte Punktmenge.
noch ein Rat
Versuchen Sie (jeder, der das liest) noch eine eigene Formulierung, die sprachlich anders als die hier angegebenen Vorschriften ist. Sprechen Sie die Vorschrift laut und deutlich. Sowas ist später Ihr Job.
Lösung 2
|
 . Wir betrachten jetzt die folgende Menge
. Wir betrachten jetzt die folgende Menge 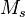 von Punkten
von Punkten  :
: 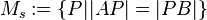 .
. ein, wählt den Radius so, dass er größer ist als die Strecke
ein, wählt den Radius so, dass er größer ist als die Strecke 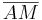 (
( ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke  .
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt
.
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt 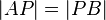 .
.
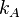 mit einem Radius
mit einem Radius  , der größer als die Hälfte der Länge von
, der größer als die Hälfte der Länge von 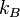 mit demselben Radius
mit demselben Radius 
 , sie ist die gesuchte Punktmenge.
, sie ist die gesuchte Punktmenge.

