Lösung von Aufgabe 2.05 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Lösung 1) |
|||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| − | Gegeben sei die Strecke <math>\overline{AB}</math>. Wir betrachten jetzt die folgende Menge <math>M_s</math> von Punkten <math>P</math>: <math>M_s:=\{P| |AP|=|PB|</math>.<br /> | + | Gegeben sei die Strecke <math>\overline{AB}</math>. Wir betrachten jetzt die folgende Menge <math>M_s</math> von Punkten <math>P</math>: <math>M_s:=\{P| |AP|=|PB|\}</math>.<br /> |
Formulieren Sie eine Konstruktionsvorschrift für <math>M_s</math>. | Formulieren Sie eine Konstruktionsvorschrift für <math>M_s</math>. | ||
==Lösung 1== | ==Lösung 1== | ||
Version vom 5. Mai 2017, 19:57 Uhr
|
Gegeben sei die Strecke Lösung 1Man zeichnet eine Strecke Lösung 2 |
 . Wir betrachten jetzt die folgende Menge
. Wir betrachten jetzt die folgende Menge 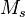 von Punkten
von Punkten  :
: 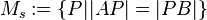 .
. ein, wählt den Radius so, dass er größer ist als die Strecke
ein, wählt den Radius so, dass er größer ist als die Strecke 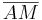 (
( ist der Mittelpunkt der Strecke
ist der Mittelpunkt der Strecke  .
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt
.
Mit derselben Vorgehensweise sticht man den Zirkel nun auch in Punkt 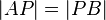 .
.

