Serie 2 Untergruppen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.4) |
*m.g.* (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
Es seien <math>[G, \odot]</math> und <math>[U,\otimes]</math> zwei Gruppen mit <math>U \subset G</math>. Warum ist <math>[U,\otimes]</math> keine Untergruppe von <math>[G, \odot]</math>? | Es seien <math>[G, \odot]</math> und <math>[U,\otimes]</math> zwei Gruppen mit <math>U \subset G</math>. Warum ist <math>[U,\otimes]</math> keine Untergruppe von <math>[G, \odot]</math>? | ||
==Aufgabe 2.2== | ==Aufgabe 2.2== | ||
| + | Es sei <math>[G, \odot]</math> eine Gruppe mit dem Einselement <math>e</math>. Beweisen Sie: <math>e</math> gehört zu jeder Untergruppe von <math>G</math>. | ||
| + | ==Aufgabe 2.3== | ||
Es sei <math>[U, \otimes]</math> eine Untergruppe von <math>[G, \otimes]</math> nach Definition 6.<br /> | Es sei <math>[U, \otimes]</math> eine Untergruppe von <math>[G, \otimes]</math> nach Definition 6.<br /> | ||
Beweisen Sie:<br /> | Beweisen Sie:<br /> | ||
| Zeile 11: | Zeile 13: | ||
:(II) <math>\forall a \in U: a^{-1} \in U</math>. | :(II) <math>\forall a \in U: a^{-1} \in U</math>. | ||
| − | ==Aufgabe 2. | + | ==Aufgabe 2.4== |
Es sei <math>[G, \otimes]</math> eine Gruppe und <math>U</math> eine nichtleere Teilmenge von <math>G</math>.<br /> | Es sei <math>[G, \otimes]</math> eine Gruppe und <math>U</math> eine nichtleere Teilmenge von <math>G</math>.<br /> | ||
Beweisen Sie:<br /> | Beweisen Sie:<br /> | ||
| Zeile 20: | Zeile 22: | ||
::ist <math>[U, \otimes]</math> eine Untergruppe von <math>[g, \otimes]</math> entsprechend Definition 6. | ::ist <math>[U, \otimes]</math> eine Untergruppe von <math>[g, \otimes]</math> entsprechend Definition 6. | ||
| − | ==Aufgabe 2. | + | ==Aufgabe 2.5== |
Beweisen Sie Satz 3. | Beweisen Sie Satz 3. | ||
| − | + | ==Aufgabe 2.6== | |
| + | Es sei <math>[G, \otimes]</math> eine Gruppe und <math>g \in G</math> mit <math>|g|=n</math>.<br /> | ||
| + | <math>U</math> sei die Menge aller Potenzen <math>g^i</math> mit <math>0<j\leq n</math>. Beweisen Sie: <math>[U, \otimes]</math> ist Untergruppe von <math>[G,\otimes]</math>. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 14. Mai 2017, 17:26 Uhr
Serie 2 Untergruppen SoSe 2017Aufgabe 2.1Es seien Aufgabe 2.2Es sei Aufgabe 2.3Es sei
Aufgabe 2.4Es sei
Aufgabe 2.5Beweisen Sie Satz 3. Aufgabe 2.6Es sei |
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) und
und ![[U,\otimes]](/images/math/9/4/e/94ec02f4088cf38ce9c1c18278b7c953.png) zwei Gruppen mit
zwei Gruppen mit 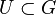 . Warum ist
. Warum ist  . Beweisen Sie:
. Beweisen Sie:  .
.
![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) nach Definition 6.
nach Definition 6.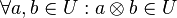 ,
,
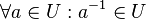 .
.
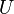 eine nichtleere Teilmenge von
eine nichtleere Teilmenge von ![[g, \otimes]](/images/math/a/7/4/a74b84c9841f61b14965df704de3f93d.png) entsprechend Definition 6.
entsprechend Definition 6.
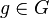 mit
mit 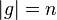 .
.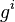 mit
mit 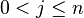 . Beweisen Sie:
. Beweisen Sie: 
