Serie 2 Untergruppen SoSe 2017
Aufgabe 2.1
Es seien ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) und und ![[U,\otimes]](/images/math/9/4/e/94ec02f4088cf38ce9c1c18278b7c953.png) zwei Gruppen mit zwei Gruppen mit 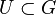 . Warum ist . Warum ist ![[U,\otimes]](/images/math/9/4/e/94ec02f4088cf38ce9c1c18278b7c953.png) keine Untergruppe von keine Untergruppe von ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) ? ?
Aufgabe 2.2
Es sei ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe mit dem Einselement eine Gruppe mit dem Einselement  . Beweisen Sie: . Beweisen Sie:  gehört zu jeder Untergruppe von gehört zu jeder Untergruppe von  . .
Aufgabe 2.3
Es sei ![[U, \otimes]](/images/math/9/4/e/94ec02f4088cf38ce9c1c18278b7c953.png) eine Untergruppe von eine Untergruppe von ![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) nach Definition 6. nach Definition 6.
Beweisen Sie:
- (I)
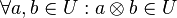 , ,
- (II)
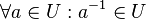 . .
Aufgabe 2.4
Es sei ![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) eine Gruppe und eine Gruppe und 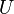 eine nichtleere Teilmenge von eine nichtleere Teilmenge von  . .
Beweisen Sie:
- Wenn
- (I)
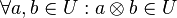 und und
- (II)
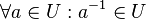
- dann
- ist
![[U, \otimes]](/images/math/9/4/e/94ec02f4088cf38ce9c1c18278b7c953.png) eine Untergruppe von eine Untergruppe von ![[g, \otimes]](/images/math/a/7/4/a74b84c9841f61b14965df704de3f93d.png) entsprechend Definition 6. entsprechend Definition 6.
Aufgabe 2.5
Beweisen Sie Satz 3.
Aufgabe 2.6
Es sei ![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) eine Gruppe und eine Gruppe und 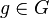 mit mit 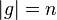 . .
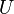 sei die Menge aller Potenzen sei die Menge aller Potenzen 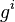 mit mit 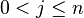 . Beweisen Sie: . Beweisen Sie: ![[U, \otimes]](/images/math/9/4/e/94ec02f4088cf38ce9c1c18278b7c953.png) ist Untergruppe von ist Untergruppe von ![[G,\otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) . .
| ![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) und
und ![[U,\otimes]](/images/math/9/4/e/94ec02f4088cf38ce9c1c18278b7c953.png) zwei Gruppen mit
zwei Gruppen mit 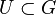 . Warum ist
. Warum ist  . Beweisen Sie:
. Beweisen Sie:  .
.
![[G, \otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) nach Definition 6.
nach Definition 6.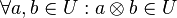 ,
,
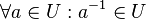 .
.
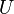 eine nichtleere Teilmenge von
eine nichtleere Teilmenge von ![[g, \otimes]](/images/math/a/7/4/a74b84c9841f61b14965df704de3f93d.png) entsprechend Definition 6.
entsprechend Definition 6.
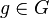 mit
mit 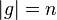 .
.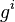 mit
mit 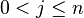 . Beweisen Sie:
. Beweisen Sie: 
