Lösung von Aufgabe 1.5 Algebra SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Lösung Aufgabe 1.5 Algebra SoSe 2017= Übungsaufgabe, Hinweise # Beginnen Sie mit Linksinvers=Rechtsinvers # Multiplizieren Sie zunächst das Linksinverse <m…“) |
*m.g.* (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;"> | ||
| + | {|width=90%| style="background-color:#CCFFCC; padding:1em" | ||
| + | | valign="top" | | ||
| + | |||
| + | |||
| + | |||
| + | =Aufgabe 1.5 Algebra SoSe 2017= | ||
| + | Beweisen Sie: In jeder Gruppe gilt: Das Linksinverse Element eines Gruppenelements <math>g</math> ist gleich dem Rechtsinversen von <math>g</math>.<br /> | ||
=Lösung Aufgabe 1.5 Algebra SoSe 2017= | =Lösung Aufgabe 1.5 Algebra SoSe 2017= | ||
Übungsaufgabe, Hinweise | Übungsaufgabe, Hinweise | ||
| Zeile 24: | Zeile 32: | ||
(VII) also <math>(g^{-1})^{-1}\cdot g^{-1}=e</math> <br /> | (VII) also <math>(g^{-1})^{-1}\cdot g^{-1}=e</math> <br /> | ||
(IX) und damit <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}=e</math> <br /> | (IX) und damit <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}=e</math> <br /> | ||
| − | (X) oder einfach: <math>g \cdot g^{-1}=e</math> und damit: Das Linksinverse <math>g^{-1}</math> von <math>g</math> ist auch sein | + | (X) oder einfach: <math>g \cdot g^{-1}=e</math> und damit: Das Linksinverse <math>g^{-1}</math> von <math>g</math> ist auch sein Rechtsinverses. |
| + | |||
| + | |||
| + | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
| + | |} | ||
| + | </div> | ||
| + | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 15. Mai 2017, 11:16 Uhr
|
Aufgabe 1.5 Algebra SoSe 2017Beweisen Sie: In jeder Gruppe gilt: Das Linksinverse Element eines Gruppenelements Lösung Aufgabe 1.5 Algebra SoSe 2017Übungsaufgabe, Hinweise
Beweis: Es sei Wir muliplizieren (III)
|
 ist gleich dem Rechtsinversen von
ist gleich dem Rechtsinversen von 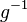 eines beliebigen Elementes
eines beliebigen Elementes 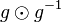

 durch das Produkt des Linksinversen vom Linksinversen von
durch das Produkt des Linksinversen vom Linksinversen von 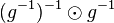 .
.
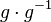
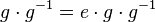
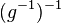
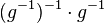
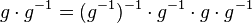
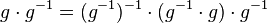
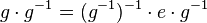
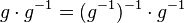
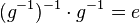
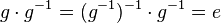
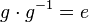 und damit: Das Linksinverse
und damit: Das Linksinverse 
