Lösung Aufgabe 5.10 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
(→Lösung 1) |
||
| Zeile 5: | Zeile 5: | ||
Es seien <math>A, B, C, D</math> vier paarweise verschiedene Punkte.<br /> Beweisen Sie: <br /> <math> \operatorname{nKomp}(A,B,C,D)\Rightarrow \operatorname{nKoll}(A,B,C)</math>. | Es seien <math>A, B, C, D</math> vier paarweise verschiedene Punkte.<br /> Beweisen Sie: <br /> <math> \operatorname{nKomp}(A,B,C,D)\Rightarrow \operatorname{nKoll}(A,B,C)</math>. | ||
=Lösung 1= | =Lösung 1= | ||
| + | Wenn nKomp (A,B,C,D), dann müssen die Punkte A,B,C eine Ebene E bilden und somit nkoll (A,B,C), da ansonsten, wenn koll (A,B,C) aus der folgenden Geraden g mit den Punkten A,B,C sich eine Ebene H mit dem Punkt D und der Geraden g bildet, was wiederum dazu führen würde, dass Komp (A,B,C,D). | ||
=Lösung 2= | =Lösung 2= | ||
Version vom 1. Juni 2017, 14:42 Uhr
Aufgabe 5.10 SoSe 2017Es seien Lösung 1Wenn nKomp (A,B,C,D), dann müssen die Punkte A,B,C eine Ebene E bilden und somit nkoll (A,B,C), da ansonsten, wenn koll (A,B,C) aus der folgenden Geraden g mit den Punkten A,B,C sich eine Ebene H mit dem Punkt D und der Geraden g bildet, was wiederum dazu führen würde, dass Komp (A,B,C,D). Lösung 2Lösung 3 |
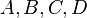vier paarweise verschiedene Punkte.
.
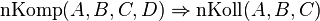