Lösung Aufgabe 5.10 SoSe 2017: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
(→Lösung 2) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| − | + | ==Aufgabe 5.10 SoSe 2017 == | |
| + | Es seien <math>A, B, C, D</math> vier paarweise verschiedene Punkte.<br /> Beweisen Sie: <br /> <math> \operatorname{nKomp}(A,B,C,D)\Rightarrow \operatorname{nKoll}(A,B,C)</math>. | ||
=Lösung 1= | =Lösung 1= | ||
| + | Wenn nKomp (A,B,C,D), dann müssen die Punkte A,B,C eine Ebene E bilden und somit nkoll (A,B,C), da ansonsten, wenn koll (A,B,C) aus der folgenden Geraden g mit den Punkten A,B,C sich eine Ebene H mit dem Punkt D und der Geraden g bildet, was wiederum dazu führen würde, dass Komp (A,B,C,D). | ||
=Lösung 2= | =Lösung 2= | ||
| + | Vorrausetzung: Nkomplanar(A,B,C,D)<br> | ||
| + | Behauptung: Nkoll(A,B,C)<br> | ||
| + | |||
| + | Kontraposition o.b.d.A. : Wenn koll(A,B,C) gilt, dann gilt komp(A,B,C,D)<br> | ||
| + | |||
| + | 1. koll(A,B,C) bedeutet es gibt eine gerade AC mit dem sich auf der geraden befindlichen Punkt B <br> | ||
| + | 2. Nun folgt aus Axiom 1.4 das 3 nkoll(A,C,D) eine Ebene E bildet. (hierbei muss nkoll(A,C,D) vorrausgesetzt sein denn sollte D kollinear mit A und C sein so ergibt sich keine Ebene)<br> | ||
| + | 3. somit komp(A,C,D) (trivial)<br> | ||
| + | 4. Da sich die Gerade AC auf der Ebene befindet muss sich auch B auf der Eben befinden.<br> | ||
| + | 5. daraus folgt Kompl(A,B,C,D)<br> | ||
=Lösung 3= | =Lösung 3= | ||
Aktuelle Version vom 1. Juni 2017, 20:26 Uhr
Aufgabe 5.10 SoSe 2017Es seien Lösung 1Wenn nKomp (A,B,C,D), dann müssen die Punkte A,B,C eine Ebene E bilden und somit nkoll (A,B,C), da ansonsten, wenn koll (A,B,C) aus der folgenden Geraden g mit den Punkten A,B,C sich eine Ebene H mit dem Punkt D und der Geraden g bildet, was wiederum dazu führen würde, dass Komp (A,B,C,D). Lösung 2Vorrausetzung: Nkomplanar(A,B,C,D) Kontraposition o.b.d.A. : Wenn koll(A,B,C) gilt, dann gilt komp(A,B,C,D) 1. koll(A,B,C) bedeutet es gibt eine gerade AC mit dem sich auf der geraden befindlichen Punkt B Lösung 3 |
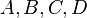vier paarweise verschiedene Punkte.
.
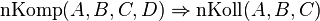