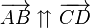Strecken, Pfeile und Pfeilklassen SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Strecken) |
*m.g.* (Diskussion | Beiträge) (→gerichtete Strecken) |
||
| Zeile 9: | Zeile 9: | ||
==Bemerkung== | ==Bemerkung== | ||
Im Gegensatz zur Definition des Begriffs Strecke in der Einführung in die Geometrie lassen wir hier zu, dass die Punkte <math>A</math> und <math>B</math> identisch sind. Der Grund hierfür liegt in der Notwendigkeit der Existenz des Nullvektors im Vektorraum der Pfeilklassen. | Im Gegensatz zur Definition des Begriffs Strecke in der Einführung in die Geometrie lassen wir hier zu, dass die Punkte <math>A</math> und <math>B</math> identisch sind. Der Grund hierfür liegt in der Notwendigkeit der Existenz des Nullvektors im Vektorraum der Pfeilklassen. | ||
| − | =gerichtete Strecken= | + | =gerichtete Strecken bzw Pfeile= |
'''Definition''': (gerichtete Strecke <math>\overrightarrow{AB}</math>) | '''Definition''': (gerichtete Strecke <math>\overrightarrow{AB}</math>) | ||
| − | ::Es sei | + | ::Es sei <math>\overline{AB}</math> eine Strecke. Wir fassen die Endpunkte zu einem geordneten Paar zusammen <math>(A,B)</math> und nennen <math>A</math> Anfangspunkt und <math>B</math> Endpunkt. Die gerichtete Strecke <math>\overrightarrow{AB}</math> bzw.der Pfeil <math>\overrightarrow{AB}</math> ist eine Strecke mit einem Anfangs und einem Endpunkt. |
| + | =Pfeilklassen= | ||
| + | '''Definition''': (Pfeilgleichheit) | ||
| + | :: Zwei Pfeile <math>\overrightarrow{AB}</math> und <math>\overrightarrow{CD}</math> stehen in der Relation pfeilgleich zueinander, wenn <math>\overline{A,C,D,B}</math> ein Parallelogramm ist. In Zeichen: <math>\overrightarrow{AB}\upuparrows \overrightarrow{CD}</math> | ||
| + | |||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Version vom 4. Juni 2017, 11:54 Uhr
StreckenDefinitionDefinition: (Strecke
BemerkungIm Gegensatz zur Definition des Begriffs Strecke in der Einführung in die Geometrie lassen wir hier zu, dass die Punkte gerichtete Strecken bzw PfeileDefinition: (gerichtete Strecke
PfeilklassenDefinition: (Pfeilgleichheit)
|
 )
)
 und
und  zwei beliebige Punkte. Unter der Strecke
zwei beliebige Punkte. Unter der Strecke 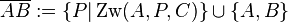 .
.
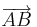 )
)
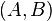 und nennen
und nennen 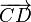 stehen in der Relation pfeilgleich zueinander, wenn
stehen in der Relation pfeilgleich zueinander, wenn 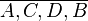 ein Parallelogramm ist. In Zeichen:
ein Parallelogramm ist. In Zeichen: