Gruppendefinition (Gleichung): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Beweis von Satz 4) |
*m.g.* (Diskussion | Beiträge) (→Beweis von Satz 4) |
||
| Zeile 11: | Zeile 11: | ||
In jeder Gruppe <math>[G, \odot]</math> gilt: Jedes Gruppenelement <math>g \in G</math> hat genau ein inverses Element. | In jeder Gruppe <math>[G, \odot]</math> gilt: Jedes Gruppenelement <math>g \in G</math> hat genau ein inverses Element. | ||
==Beweis von Satz 4== | ==Beweis von Satz 4== | ||
| − | Es sei <math>g \in G</math> eine Gruppe mit dem Einslement <math>e</math>. Nach der Definition des Begriffs Gruppe hat <math>g</math> in <math>G</math> ein Inverses <math>g_1^{-1}</math> bezüglich <math>\odot</math>. Wir nehmen an, <math>g</math> hat in <math>G</math> ein weiteres Inverses <math>g_2^{-1}</math>, das natürlich von <math>g_1^{-1}</math> verschieden ist. Nach Satz 1 wissen wir, dass <math>g_1{-1}</math> und <math>g_2^{-1}</math> von links und von rechts invers zu <math>g</math> bzgl. <math>\odot</math> sind. Die triviale Gleichung <math>(I) e=e</math> "pumpen" wir zu <math>(II) g \odot g_1^{-1} = g \odot g_2{-1}</math> auf. (II) multiplizieren wir auf beiden Seiten von links mit <math>g_1^{-1}</math> und erhalten <math>g_1^{-1} \odot g \odot g_1^{-1}= g_1^{-1} \odot g \odot g_2{-1}</math>. (III) verkürzt sich zu <math>g_1^{-1}=g_2{-1}</math>, was ein Widerspruch zu unserer Annahme <math>g_1^{-1} \neq g_2^{-1}</math> ist. | + | Es sei <math>g \in G</math> eine Gruppe mit dem Einslement <math>e</math>. Nach der Definition des Begriffs Gruppe hat <math>g</math> in <math>G</math> ein Inverses <math>g_1^{-1}</math> bezüglich <math>\odot</math>. Wir nehmen an, <math>g</math> hat in <math>G</math> ein weiteres Inverses <math>g_2^{-1}</math>, das natürlich von <math>g_1^{-1}</math> verschieden ist. Nach Satz 1 wissen wir, dass <math>g_1^{-1}</math> und <math>g_2^{-1}</math> von links und von rechts invers zu <math>g</math> bzgl. <math>\odot</math> sind. <br /> |
| + | |||
| + | Die triviale Gleichung <math>(I) e=e</math> "pumpen" wir zu <math>(II) g \odot g_1^{-1} = g \odot g_2{-1}</math> auf. <br /> | ||
| + | |||
| + | <math>(II)</math> multiplizieren wir auf beiden Seiten von links mit <math>g_1^{-1}</math> und erhalten <math>(III) g_1^{-1} \odot g \odot g_1^{-1}= g_1^{-1} \odot g \odot g_2{-1}</math>.<br /> | ||
| + | |||
| + | <math>(III)</math> verkürzt sich zu <math>g_1^{-1}=g_2^{-1}</math>, was ein Widerspruch zu unserer Annahme <math>g_1^{-1} \neq g_2^{-1}</math> ist. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Version vom 25. November 2017, 13:16 Uhr
Eindeutigkeit des EinslementesSatz 3Jede Gruppe hat genau ein Einslement. Beweis von Satz 3Es sei Eindeutigkeit der inversen ElementeSatz 4In jeder Gruppe Beweis von Satz 4Es sei Die triviale Gleichung
|
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe. Nach der Definition des Begriffs Gruppe hat
eine Gruppe. Nach der Definition des Begriffs Gruppe hat 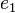 . Es bleibt zu zeigen, dass
. Es bleibt zu zeigen, dass 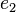 hat. Wir nehmen an es gibt
hat. Wir nehmen an es gibt 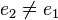 . Nach Satz 2 sind
. Nach Satz 2 sind 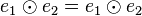 . Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente
. Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente 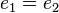 .
.
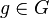 hat genau ein inverses Element.
hat genau ein inverses Element.
 . Nach der Definition des Begriffs Gruppe hat
. Nach der Definition des Begriffs Gruppe hat  in
in  ein Inverses
ein Inverses 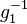 bezüglich
bezüglich  . Wir nehmen an,
. Wir nehmen an, 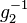 , das natürlich von
, das natürlich von 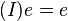 "pumpen" wir zu
"pumpen" wir zu 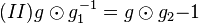 auf.
auf. 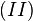 multiplizieren wir auf beiden Seiten von links mit
multiplizieren wir auf beiden Seiten von links mit 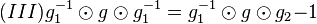 .
.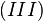 verkürzt sich zu
verkürzt sich zu 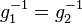 , was ein Widerspruch zu unserer Annahme
, was ein Widerspruch zu unserer Annahme 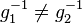 ist.
ist.

