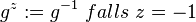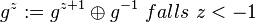Gruppenordnung, Ordnung eines Gruppenelements: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Definition Potenz g^z eines Gruppenelements für z \in \mathbb{Z}, z \geq 0) |
*m.g.* (Diskussion | Beiträge) (→Beispiel 1: [\mathbb{Z}_5 , \oplus]) |
||
| Zeile 23: | Zeile 23: | ||
====Beispiel 1: <math>[\mathbb{Z}_5 , \oplus]</math>==== | ====Beispiel 1: <math>[\mathbb{Z}_5 , \oplus]</math>==== | ||
*<math>\overline{2}^3=\overline{2} \oplus \overline{2} \oplus \overline{2}= \overline{2+2+2} = \overline{6}= \overline{1}</math><br /> | *<math>\overline{2}^3=\overline{2} \oplus \overline{2} \oplus \overline{2}= \overline{2+2+2} = \overline{6}= \overline{1}</math><br /> | ||
| − | *<math>\overline{2}^{-3}=\overline{3}^3=\overline{3} \oplus \overline{3} \oplus{3} = \overline{3+3+3} = \overline{9} = \overline{4}</math> | + | *<math>\overline{2}^{-3}=\overline{3}^3=\overline{3} \oplus \overline{3} \oplus \overline{3} = \overline{3+3+3} = \overline{9} = \overline{4}</math> |
| + | |||
==Definition Potenz <math>g^z</math> eines Gruppenelements für <math>z \in \mathbb{Z}, z \geq 0</math>== | ==Definition Potenz <math>g^z</math> eines Gruppenelements für <math>z \in \mathbb{Z}, z \geq 0</math>== | ||
Es sei <math>[G, \oplus]</math> eine Gruppe mit dem Neutralelement <math>n</math>. Für beliebige Elemente <math>g \in G</math> und ganze Zahlen <math>z \geq 0</math> definieren wir: | Es sei <math>[G, \oplus]</math> eine Gruppe mit dem Neutralelement <math>n</math>. Für beliebige Elemente <math>g \in G</math> und ganze Zahlen <math>z \geq 0</math> definieren wir: | ||
Version vom 28. November 2017, 11:28 Uhr
Die Ordnung einer GruppeDefinition (GruppenordnungEs sei BeispielePotenzschreibweisen in GruppenAus der Schule bekanntPotenzen sind aus der Schule bezüglich der Multiplikation reeller Zahlen bekannt: Verallgemeinerung auf beliebige GruppenBeispiele Beispiel 1:
|
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe. Unter der Ordnung
eine Gruppe. Unter der Ordnung 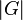 von
von  .
.
![[\mathbb{Z}_5,\oplus]: |\mathbb{Z}_5|=5](/images/math/0/a/d/0ad5cf016cd8a3a2358e7ccad3890034.png)
![[\mathbb{Z}_5,\odot]: |\mathbb{Z}_5|=4](/images/math/6/c/2/6c20f25aff626bd643056ca1a478936a.png)
![[\mathbb{Q}, +] : |\mathbb{Q}|= \infty](/images/math/6/f/2/6f2a1357b47ed4dca59f57d2db3373cf.png)
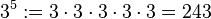
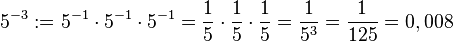
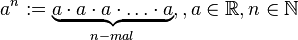
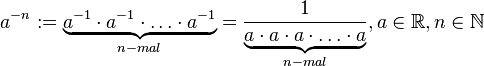
![[\mathbb{Z}_5 , \oplus]](/images/math/3/e/5/3e50b5df0a8bed28c771686d3c139ed4.png)
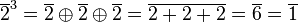
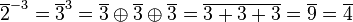
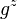 eines Gruppenelements für
eines Gruppenelements für 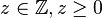
![[G, \oplus]](/images/math/7/6/a/76a5019aba25ee8b54b799a29a626d33.png) eine Gruppe mit dem Neutralelement
eine Gruppe mit dem Neutralelement  . Für beliebige Elemente
. Für beliebige Elemente 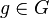 und ganze Zahlen
und ganze Zahlen 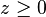 definieren wir:
definieren wir:
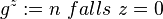
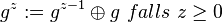
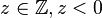
 eine beliebiges Gruppenelement und
eine beliebiges Gruppenelement und 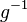 sein Inverses in
sein Inverses in