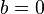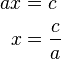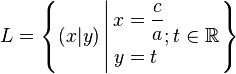Allgemeine lineare Gleichung mit zwei Variablen: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „===ax + by + c = 0=== <math> \begin{align} ax+by=c \\ a, b, c \in \mathbb{R} \\ x, y \in \mathbb{R}, \end{align} </math><br /> <iframe scrolling="no" title="Li…“) |
Version vom 3. Mai 2018, 15:15 Uhr
Inhaltsverzeichnis |
ax + by + c = 0
[ www.geogebra.org is not an authorized iframe site ]
Grafische Veranschaulichung der Lösungsmenge einer Gleichung vom Typ ax+by=c
Es seien 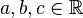 , beliebig aber fest,
, beliebig aber fest, 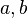 nicht gleichzeitig
nicht gleichzeitig 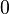 ,
,
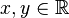 , variabel.
, variabel.
Wir untersuchen die Gleichung
(I) 
Satz 1:
- Die Gleichung (II)
 beschreibt die Menge aller Punkte einer Geraden in der reellen Zahlenebene.
beschreibt die Menge aller Punkte einer Geraden in der reellen Zahlenebene.
Beweis:
Aus der Schule ist die folgende Gleichung für Geraden bekannt: 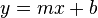 ,
, 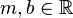 , beliebig aber fest,
, beliebig aber fest, 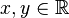 variabel.
Wir führen zwei Beweise:
variabel.
Wir führen zwei Beweise:
- Wir zeigen, dass jede Gleichung vom Typ (I) durch äquivalente Umformungen in eine Gleichung vom Typ (II) überführt werden kann.
- Wir zeigen, dass umgekehrt (fast) jede Gleichung vom Typ (II) durch äquivalente Umformungen in den Typ (I) überführt werden können.
Ausführung des Beweises: Übungsaufgaben 1.1 und 1.2 in Serie 1: Geraden in der Ebene, zwei Gleichungen mit zwei Unbekannten SoSe 2018
Algebraische Beschreibung der Lösungsmenge einer Gleichung der Form 
Voraussetzung
Wir schließen aus, dass  und
und  gleichzeitig
gleichzeitig 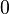 sind:
sind: 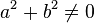
Fall 1: 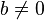
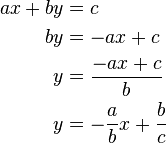
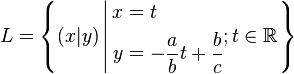
Falls 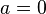 vereinfacht sich die Lösungsmenge
vereinfacht sich die Lösungsmenge  zu:
zu:
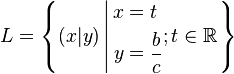
Fall 2: