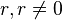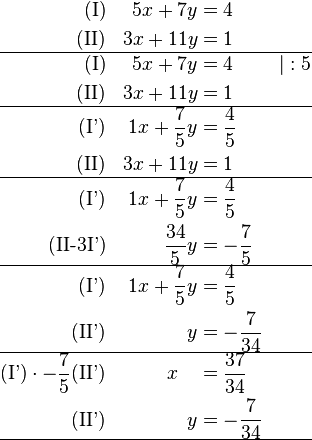Das Additionsverfahren: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „====Äquivalenzumformungen für Lineare Gleichungssysteme==== * Vertauschen zweier Gleichungen * Multiplikation einer Gleichung mit einer reellen Zahl <math>r,…“) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> | ||
| + | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- hier drüber nichts eintragen ---> | ||
| + | |||
====Äquivalenzumformungen für Lineare Gleichungssysteme==== | ====Äquivalenzumformungen für Lineare Gleichungssysteme==== | ||
* Vertauschen zweier Gleichungen | * Vertauschen zweier Gleichungen | ||
| Zeile 29: | Zeile 34: | ||
<br /> | <br /> | ||
<iframe scrolling="no" title="Beispiel01" src="https://www.geogebra.org/material/iframe/id/sNHCfFDn/width/1000/height/726/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="1000px" height="726px" style="border:0px;"> </iframe> | <iframe scrolling="no" title="Beispiel01" src="https://www.geogebra.org/material/iframe/id/sNHCfFDn/width/1000/height/726/border/888888/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="1000px" height="726px" style="border:0px;"> </iframe> | ||
| + | |||
| + | |||
| + | |||
| + | <!--- hier drunter nichts eintragen ---> | ||
| + | [[Kategorie:Linalg]] | ||
| + | |||
| + | |} | ||
| + | </div> | ||
Aktuelle Version vom 3. Mai 2018, 15:25 Uhr
Äquivalenzumformungen für Lineare Gleichungssysteme
Beispiel 1
|