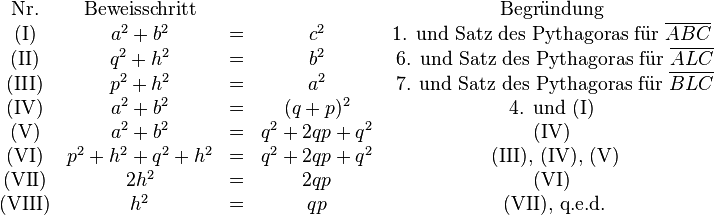Lösung von Aufgabe 2.8 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) (→Lösung) |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
<!--- Was hier drüber steht muss stehen bleiben ---> | <!--- Was hier drüber steht muss stehen bleiben ---> | ||
| + | =Aufgabe 2.8 SoSe 2018= | ||
| + | Der Höhensatz für rechtwinklige Dreiecke lautet:<br /> | ||
| + | '''Satz: (Höhensatz)'''<br /> | ||
| + | : In jedem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrates über der Höhe <math>h_c</math> auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten <math>q</math> und <math>p</math> entsprechen. <br /> | ||
| + | Kurz: <math>h_c^2=q \cdot p</math><br /> | ||
| − | + | Beweisen Sie den Höhensatz unter Verwendung des Satzes von Pythagoras.<br /> | |
| + | =Lösung= | ||
| + | # Es sei <math> \overline{ABC}</math> ein rechtwinkliges Dreieck mit dem rechten Winkel <math>\gamma = \angle ACB</math>. | ||
| + | # Die Höhe <math>h</math> von <math>C</math> auf die Seite <math>c=\overline{AB}</math> habe auf <math>c</math> den Fußpunkt <math>~L</math>. | ||
| + | # <math> ~L</math> teilt die Hypotenuse <math>c</math> in die beiden Hypotenusenabschnitte <math>q:= \overline{AL}</math> und <math>p:= \overline{LB}</math>. | ||
| + | # Es gilt also <math>c=q+p</math>. | ||
| + | # Weil die Höhe <math>h</math> senkrecht auf der Hypotenuse <math>c</math> steht, entstehen die zwei rechtwinklige Teildreiecke <math>\overline{ALC}</math> und <math>\overline{BLC}</math>. | ||
| + | # Im rechtwinkligen Teildreieck <math>\overline{ALC}</math> ist <math>a= \overline{AC}</math> die Hypotenuse und <math>\angle ALC</math> der rechte Winkel. | ||
| + | # Im rechtwinkligen Teildreieck <math>\overline{BLC}</math> ist <math>b= \overline{BC}</math> die Hypotenuse und <math>\angle BLC</math> der rechte Winkel. | ||
| + | <math> | ||
| + | \begin{matrix} | ||
| + | \text{Nr.} & \text{Beweisschritt} & ~ & ~ & \text{Begründung} \\ | ||
| + | \text{(I)} & a^2+b^2 & = &c^2 & \text{1. und Satz des Pythagoras für } \overline{ABC} \\ | ||
| + | \text{(II)} & q^2 + h^2 & = & b^2 & \text{ 6. und Satz des Pythagoras für } \overline{ALC} \\ | ||
| + | \text{(III)} & p^2 + h^2 & = & a^2 & \text{ 7. und Satz des Pythagoras für } \overline{BLC} \\ | ||
| + | \text{(IV)} & a^2+b^2 &= &(q+p)^2 & \text{4. und (I)} \\ | ||
| + | \text{(V)} & a^2 + b^2 &= & q^2 +2qp + q^2 & \text{(IV)} \\ | ||
| + | \text{(VI)} & p^2 + h^2 + q^2 + h^2 &= & q^2 +2qp + q^2 & \text{ (III), (IV), (V)} \\ | ||
| + | \text{(VII)} & 2h^2 &= & 2qp & \text{(VI)} \\ | ||
| + | \text{(VIII)} & h^2 &= & qp & \text{ (VII), q.e.d.} \\ | ||
| + | \end{matrix} | ||
| + | </math> | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 22. Mai 2018, 12:26 Uhr
Aufgabe 2.8 SoSe 2018Der Höhensatz für rechtwinklige Dreiecke lautet:
Kurz: Beweisen Sie den Höhensatz unter Verwendung des Satzes von Pythagoras. Lösung
|
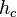 auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten
auf die Hypotenuse so groß, wie der Flächeninhalt des Rechtecks, dessen Seitenlängen den Hypotenusenabschnitten 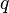 und
und  entsprechen.
entsprechen. 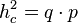
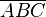 ein rechtwinkliges Dreieck mit dem rechten Winkel
ein rechtwinkliges Dreieck mit dem rechten Winkel 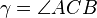 .
.
 von
von  auf die Seite
auf die Seite 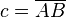 habe auf
habe auf  den Fußpunkt
den Fußpunkt 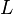 .
.
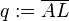 und
und 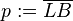 .
.
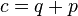 .
.
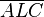 und
und 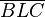 .
.
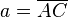 die Hypotenuse und
die Hypotenuse und 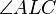 der rechte Winkel.
der rechte Winkel.
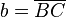 die Hypotenuse und
die Hypotenuse und 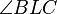 der rechte Winkel.
der rechte Winkel.