Videos zur Winkelmessung: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Supplementaxiom) |
*m.g.* (Diskussion | Beiträge) (→Rechte Winkel) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 23: | Zeile 23: | ||
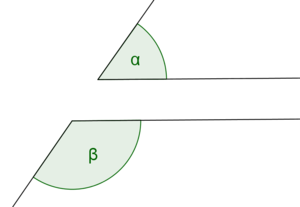
=Nebenwinkel= | =Nebenwinkel= | ||
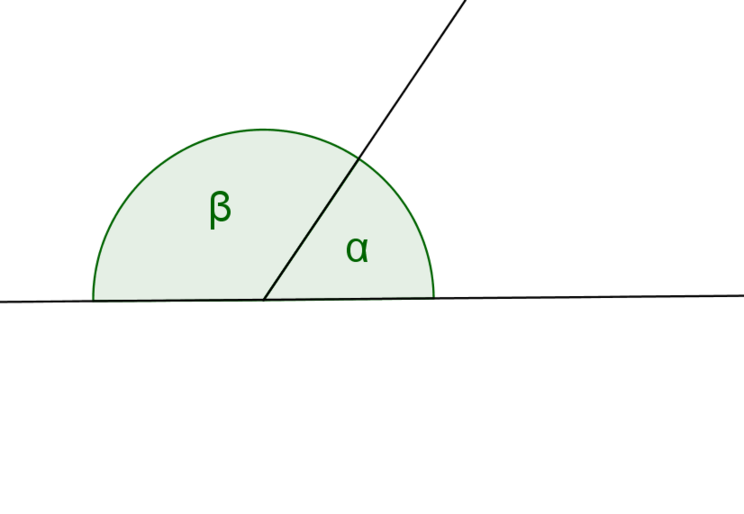
| + | ==Beispiel== | ||
| + | [[Datei:Nebenwinkel Beispiel 01.png|Beispiel für Nebenwinkel]] | ||
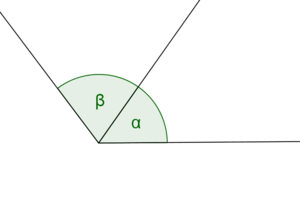
| + | ==Gegenbeispiel 1== | ||
| + | [[Datei:Nebenwinkel Gegenbeispiel 01.png|Gegenbeisspiel für Nebenwinkel]] | ||
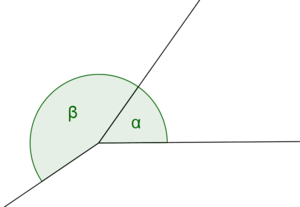
| + | ==Gegenbeispiel 2== | ||
| + | [[Datei:Nebenwinkel Gegenbeispiel 04.png|Gegenbeisspiel für Nebenwinkel]] | ||
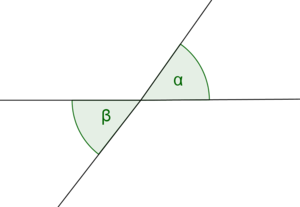
| + | ==Gegenbeispiel 3== | ||
| + | [[Datei:Nebenwinkel Gegenbeisppiel 05.png|Gegenbeisspiel für Nebenwinkel]] | ||
| + | ==Gegenbeispiel 4== | ||
| + | [[Datei:Nebenwinkel Gegenbespiel 02.png| Gegenbeisspiel für Nebenwinkel]] | ||
=Supplementaxiom= | =Supplementaxiom= | ||
| Zeile 30: | Zeile 40: | ||
=Rechte Winkel= | =Rechte Winkel= | ||
| + | ohne Video | ||
| + | ==Rechte Winkel:== | ||
| + | Ein Winkel, der so groß ist, wie einer seiner Nebenwinkel, heißt rechter Winkel. | ||
=Existenz von rechten Winkeln= | =Existenz von rechten Winkeln= | ||
<iframe width="560" height="315" src="https://www.youtube.com/embed/pNpaFZwMoC8" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | <iframe width="560" height="315" src="https://www.youtube.com/embed/pNpaFZwMoC8" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | ||
| − | + | =Begriff der Winkelhalbierenden= | |
| + | <iframe width="560" height="315" src="https://www.youtube.com/embed/lRHJTto_io4" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe> | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 10. Juni 2018, 13:33 Uhr
Winkelbegriff[ www.youtube.com is not an authorized iframe site ] Winkelmaßaxiom[ www.youtube.com is not an authorized iframe site ] WinkelkonstruktionsaxiomLeider ohne Video. Das Axiom:Sei Winkeladditionsaxiom[ www.youtube.com is not an authorized iframe site ] Supplementärwinkel[ www.youtube.com is not an authorized iframe site ] NebenwinkelBeispiel
Gegenbeispiel 1
Gegenbeispiel 2
Gegenbeispiel 3
Gegenbeispiel 4
SupplementaxiomOhne Video Das AxiomNebenwinkel sind supplementär. Rechte Winkelohne Video Rechte Winkel:Ein Winkel, der so groß ist, wie einer seiner Nebenwinkel, heißt rechter Winkel. Existenz von rechten Winkeln[ www.youtube.com is not an authorized iframe site ] Begriff der Winkelhalbierenden[ www.youtube.com is not an authorized iframe site ] |
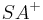ein Strahl in der Ebene 
.
Zu jeder reellen Zahl 
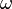mit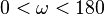 
gibt es in 
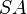bestimmten Halbebenen genau einen Strahl 
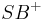mit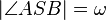 
.
