Lösung von Aufgabe 11.8: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: VSS: m ist die Mittelsenkrechte von <math>\overline{AB}</math> <br /> Beh: <math> a \cong b </math><br /> {| class="wikitable " |+ Beweis ! Nr. ! Beweisschritt ! Beg...) |
(→Lösung 1) |
||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | VSS: m ist die Mittelsenkrechte von <math>\overline{AB}</math> <br /> | + | Beweisen Sie Satz VII.6 b: |
| + | <br />Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand.<br /> | ||
| + | |||
| + | |||
| + | == Lösung 1 == | ||
| + | |||
| + | VSS: m ist die Mittelsenkrechte von <math>\overline{AB}</math>, <math>P \in m</math><br /> | ||
Beh: <math> a \cong b </math><br /> | Beh: <math> a \cong b </math><br /> | ||
| Zeile 10: | Zeile 16: | ||
! style="background: #FFDDDD;"|(I) | ! style="background: #FFDDDD;"|(I) | ||
| <math>\overline{AM} \cong \overline{BM}</math> | | <math>\overline{AM} \cong \overline{BM}</math> | ||
| − | | (Existenz und Eindeutigkeit Mittelpunkt) | + | | (Existenz und Eindeutigkeit Mittelpunkt), (Def. Mittelsenkrechte) |
|- | |- | ||
! style="background: #FFDDDD;"|(II) | ! style="background: #FFDDDD;"|(II) | ||
| es existiert ein Punkt <math> P \in m</math> | | es existiert ein Punkt <math> P \in m</math> | ||
| − | | | + | | (VSS) |
|- | |- | ||
! style="background: #FFDDDD;"|(III) | ! style="background: #FFDDDD;"|(III) | ||
| <math> \angle AMP \cong \angle BMP </math> | | <math> \angle AMP \cong \angle BMP </math> | ||
| − | | Definition Mittelsenkrechte | + | | (Definition Mittelsenkrechte), (Def. Nebenwinkel), (Supplementaxiom) |
|- | |- | ||
! style="background: #FFDDDD;"|(IV) | ! style="background: #FFDDDD;"|(IV) | ||
| <math>\overline{MP} \cong \overline{MP}</math> | | <math>\overline{MP} \cong \overline{MP}</math> | ||
| − | | trivial | + | | (trivial) |
|- | |- | ||
! style="background: #FFDDDD;"|(V) | ! style="background: #FFDDDD;"|(V) | ||
| Zeile 33: | Zeile 39: | ||
|} | |} | ||
| − | + | --> Beh ist wahr.<br /> | |
| + | qed --[[Benutzer:Löwenzahn|Löwenzahn]] 09:36, 3. Jul. 2010 (UTC) | ||
| + | |||
| + | Der Fall P=M sollte bei Schritt IV vielleicht noch ergänzt werden. Wenn P=M, dann hat P den gleichen Abstand zu A und B (Begründung Schritt I) | ||
| + | --[[Benutzer:Principella|Principella]] 17:03, 12. Jul. 2010 (UTC) | ||
| + | |||
| + | <br /> | ||
| + | Bei Schritt (III) würde ich als Begründung "Def. Mittelsenkrechte", "Def. senkrecht" und "Def. rechte winkel" aufführen, da man von Def. Mittelsenkrechte nicht unmittelbar schließen kann, dass die Winkel Nebenwinkel und supplementär sind! Ich habe das nochmal in 3 Extraschritte | ||
| + | aufgeteilt. --[[Benutzer:TheGeosi|TheGeosi]] 09:41, 15. Jul. 2010 (UTC) | ||
Aktuelle Version vom 15. Juli 2010, 11:41 Uhr
Beweisen Sie Satz VII.6 b:
Wenn ein Punkt 
zur Mittelsenkrechten der Strecke 
gehört, dann hat er zu den Punkten 
und 
ein und denselben Abstand.
Lösung 1
VSS: m ist die Mittelsenkrechte von , 
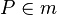
Beh: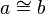 
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) |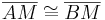 
|
(Existenz und Eindeutigkeit Mittelpunkt), (Def. Mittelsenkrechte) |
| (II) | es existiert ein Punkt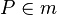
|
(VSS) |
| (III) |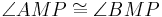 
|
(Definition Mittelsenkrechte), (Def. Nebenwinkel), (Supplementaxiom) |
| (IV) |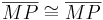 
|
(trivial) |
| (V) |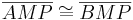 
|
(I), (III), (IV), (SWS) |
| (VI) | |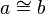
(V), (Def Dreieckskongruenz) |
--> Beh ist wahr.
qed --Löwenzahn 09:36, 3. Jul. 2010 (UTC)
Der Fall P=M sollte bei Schritt IV vielleicht noch ergänzt werden. Wenn P=M, dann hat P den gleichen Abstand zu A und B (Begründung Schritt I) --Principella 17:03, 12. Jul. 2010 (UTC)
Bei Schritt (III) würde ich als Begründung "Def. Mittelsenkrechte", "Def. senkrecht" und "Def. rechte winkel" aufführen, da man von Def. Mittelsenkrechte nicht unmittelbar schließen kann, dass die Winkel Nebenwinkel und supplementär sind! Ich habe das nochmal in 3 Extraschritte
aufgeteilt. --TheGeosi 09:41, 15. Jul. 2010 (UTC)
